A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope. Find(i) the area of that part of the field in which the horse can graze.(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m.
To solve the problem step by step, we will break it down into two parts as given in the question.
Part (i): Area of Grazing with a 5 m Rope
1. Identify the parameters:
- The side of the square field = 15 m
- Length of the rope = 5 m
2. Determine the grazing area:
The horse can graze in a quarter-circle area since it is tied at one corner of the square field. The radius of this quarter-circle is equal to the length of the rope, which is 5 m.
3. Calculate the area of the quarter-circle:
The formula for the area of a circle is:
Area=πr2
For a quarter-circle, the area will be:
Area of quarter-circle=14πr2
Substituting r=5 m:
Area=14×227×(52)=14×227×25
=55028=27514≈19.64 m2
Part (ii): Increase in Grazing Area with a 10 m Rope
1. Identify the new parameters:
- New length of the rope = 10 m
2. Determine the new grazing area:
The horse can still graze in a quarter-circle area, but now the radius is 10 m.
3. Calculate the area of the new quarter-circle:
Using the same formula:
Area of quarter-circle=14πr2
Substituting r=10 m:
Area=14×227×(102)=14×227×100
=220028=110014≈78.57 m2
4. Calculate the increase in grazing area:
Increase in area=New area−Old area=78.57 m2−19.64 m2
=58.93 m2
Final Answers:
(i) The area of the part of the field in which the horse can graze with a 5 m rope is approximately 19.64 m².
(ii) The increase in the grazing area if the rope were 10 m long instead of 5 m is approximately 58.93 m².
- The side of the square field = 15 m
- Length of the rope = 5 m
The horse can graze in a quarter-circle area since it is tied at one corner of the square field. The radius of this quarter-circle is equal to the length of the rope, which is 5 m.
The formula for the area of a circle is:
Area=πr2
For a quarter-circle, the area will be:
Area of quarter-circle=14πr2
Substituting r=5 m:
Area=14×227×(52)=14×227×25
=55028=27514≈19.64 m2
- New length of the rope = 10 m
The horse can still graze in a quarter-circle area, but now the radius is 10 m.
Using the same formula:
Area of quarter-circle=14πr2
Substituting r=10 m:
Area=14×227×(102)=14×227×100
=220028=110014≈78.57 m2
Increase in area=New area−Old area=78.57 m2−19.64 m2
=58.93 m2
(i) The area of the part of the field in which the horse can graze with a 5 m rope is approximately 19.64 m².
(ii) The increase in the grazing area if the rope were 10 m long instead of 5 m is approximately 58.93 m².
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.15videos
AREAS RELATED TO CIRCLES
- BOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES6videos
AREAS RELATED TO CIRCLES
- BOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES6videos
AREAS RELATED TO CIRCLES
- BOOK - NCERT ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - All Questions65videos
ARITHMETIC PROGRESSIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Four square flower beds, each of side 5m, are dug on a piece of land 10m long and 15m wide. What is the area of the remaining part of the land?
A60sq.mB50sq.mC30sq.mD80sq.m
A horse is tied to a pole with 28 m long string. Find the area where the horse can graze. (Takeπ=227 ).
View SolutionA horse is tied to a pole with 28 m long string. Find the area where the horse can graze. (Takeπ=227 ).
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
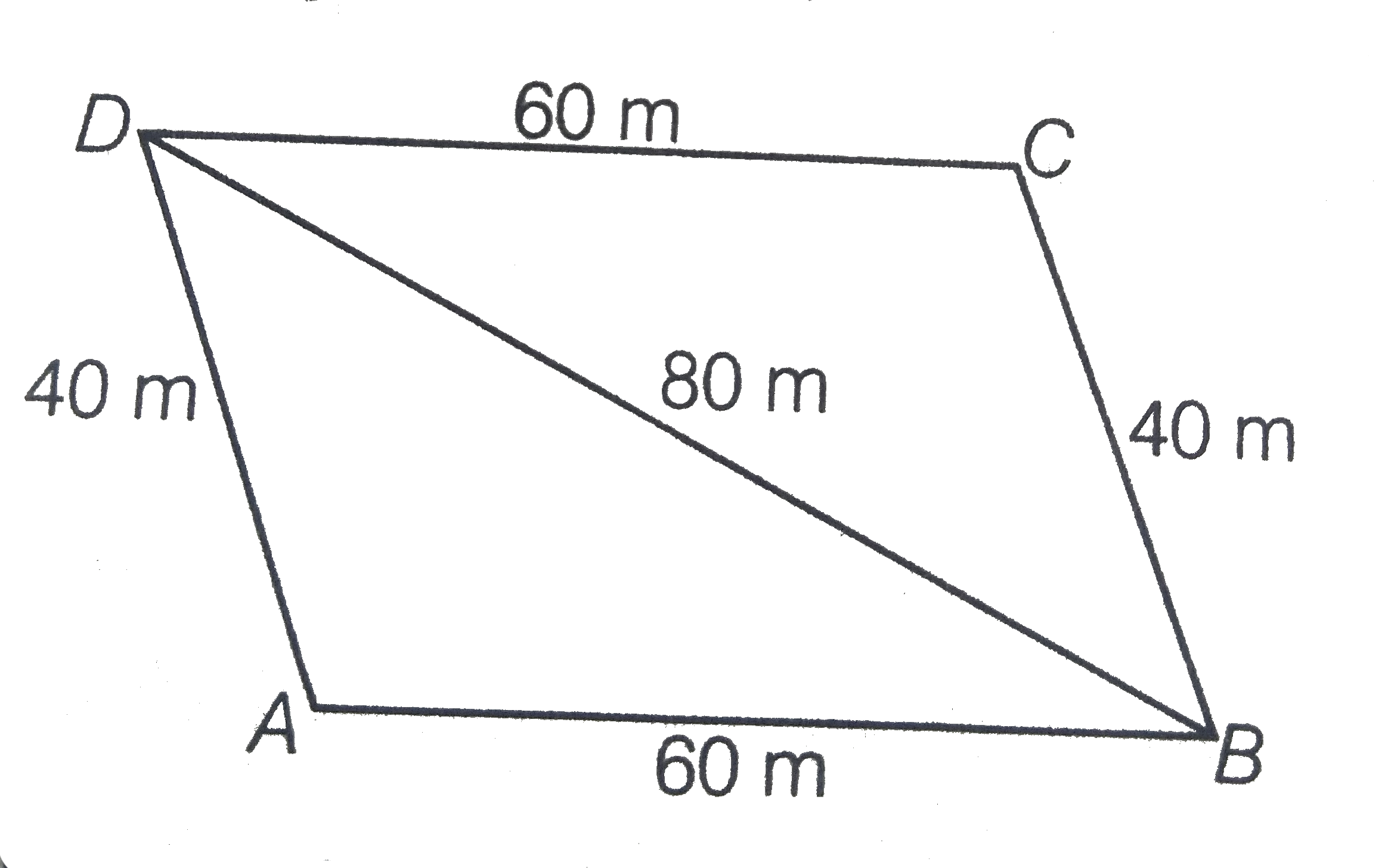 View Solution
View SolutionFive square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
View SolutionEach side of a square is 623 m long. Find its area.
View SolutionEach side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.
View SolutionA floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
View Solution

