A large right circular cone is made out of a solid cube edge 9 cm. Find the volume of the remaining solid.
To find the volume of the remaining solid after a cone is carved out of a cube, we can follow these steps:
Step 1: Find the volume of the cube
The volume V of a cube is given by the formula:
V=side3
Given that the edge of the cube is 9 cm, we can calculate:
Vcube=93=729 cm3
Step 2: Determine the dimensions of the cone
The cone is inscribed in the cube. The radius r of the cone is half the side length of the cube:
r=side2=92=4.5 cm
The height h of the cone is equal to the side of the cube:
h=9 cm
Step 3: Calculate the volume of the cone
The volume V of a cone is given by the formula:
V=13πr2h
Substituting the values we found:
Vcone=13π(4.5)2(9)
Calculating (4.5)2:
(4.5)2=20.25
Now substituting back:
Vcone=13π(20.25)(9)=13π(182.25)
Calculating:
Vcone=60.75π cm3
Using π≈3.14:
Vcone≈60.75×3.14≈190.185 cm3
Step 4: Find the volume of the remaining solid
The volume of the remaining solid is the volume of the cube minus the volume of the cone:
Vremaining=Vcube−Vcone
Substituting the values:
Vremaining=729−190.185≈538.815 cm3
Final Answer
The volume of the remaining solid is approximately 538.815 cm3.
---
The volume V of a cube is given by the formula:
V=side3
Given that the edge of the cube is 9 cm, we can calculate:
Vcube=93=729 cm3
The cone is inscribed in the cube. The radius r of the cone is half the side length of the cube:
r=side2=92=4.5 cm
The height h of the cone is equal to the side of the cube:
h=9 cm
The volume V of a cone is given by the formula:
V=13πr2h
Substituting the values we found:
Vcone=13π(4.5)2(9)
Calculating (4.5)2:
(4.5)2=20.25
Now substituting back:
Vcone=13π(20.25)(9)=13π(182.25)
Calculating:
Vcone=60.75π cm3
Using π≈3.14:
Vcone≈60.75×3.14≈190.185 cm3
The volume of the remaining solid is the volume of the cube minus the volume of the cone:
Vremaining=Vcube−Vcone
Substituting the values:
Vremaining=729−190.185≈538.815 cm3
The volume of the remaining solid is approximately 538.815 cm3.
Topper's Solved these Questions
- SURFACE AREA AND VOLUME BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - PRACTICE TEST ( SECTION-D)
1 Videos
- SURFACE AREA AND VOLUME BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - PRACTICE TEST ( SECTION-B)
3 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Practice -Test
5 Videos
- TRIANGLEBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-II
25 Videos
Similar Questions
The largest cone is curved out from one face of solid cube of side 21 cm find the volume of the remaining solid.
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid. (Take π=3.14)
View Solution
Knowledge Check
The diamtere of a right circular cone in 14 m , while its slant height is 9 m. Find the volume of the cone.
A49π√323m3B50π√323m3C349π√32m3Dπ√329m3
From a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
View SolutionThe largest possible right circular cone is cut out of a cube of edge r cm. what is the volume of cone?
View SolutionA cone of maximum size is carved out from a solid cube of side 14 cm. Find the total surface area of the remaining solid left out.
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the the same height and same base is removed . find the volume of the remaining solid
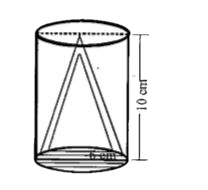
View SolutionA cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the remaining solid after the cone is carved out.
View SolutionThe area of the base of a right circular cone is 314cm2 and its height is 15cm. Find the volume of the cone.
View SolutionFrom a solid circular cylinder with height 10 cm and radius of the base 6 cm, a circular cone of the same height and same base is removed. Find the volume of remaining solid and also find the whole surface area.
View Solution
