A line L passing through the focus of the parabola y2=4(x−1) intersects the parabola at two distinct points. If m is the slope of the line L,then Solution in Bengali
−1<m<1
m<−1orm>1
m∈R
none of these
The correct Answer is:D
Any line passing through the focus other than the axis always meets the parabols at two distinct points.
Hence, m∈R−{0}.
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWER TYPE )
26 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - LINKED COMPREHENSION TYPE
45 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Concept Applications Exercise 5.7
9 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE PUBLICATIONCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
If the focus of the parabola x2−ky+3=0 is (0,2), then a values of k is (are)
View SolutionA tangent is drawn at any point P(t) on the parabola y2=8x and on it is takes a point Q(α,β) from which a pair of tangent QA and OB are drawn to the circle x2+y2=8. Using this information, answer the following questions :
The locus of the point of concurrecy of the chord of contact AB of the circle x2+y2=8 is
View SolutionIf the normal to the parabola y2=4ax at point t1 cuts the parabola again at point t2 , then prove that t22≥8.
View SolutionThe distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
View SolutionGiven are six 0's, five 1's and four 2's . Consider all possible permutations of all these numbers. [A permutations can have its leading digit 0].
How many permutations have the first 0 preceding the first 1 ?
(a) 15C4×10C5 (b) 15C5×10C4 (c) 15C6×10C5 (d) 15C5×10C5
View SolutionIf xl+ym=1 is any line passing through the intersection point of the lines xa+yb=1 and xb+ya=1 then prove that 1l+1m=1a+1b
View SolutionStatement 1: The point of intersection of the tangents at three distinct points A,B,andC on the parabola y2=4x can be collinear. Statement 2: If a line L does not intersect the parabola y2=4x, then from every point of the line, two tangents can be drawn to the parabola.
View SolutionA line L passing through the focus of the parabola y2=4(x−1) intersects the parabola at two distinct points. If m is the slope of the line L, then −1<m<1 (b) m<−1 or m>1 m∈R (d) none of these
View SolutionFind the equation of the parabola whose focus is (0,0) and the vertex is the point of intersection of the lines x+y=1 and x−y=3.
View SolutionA line L passing through the focus of the parabola (y−2)2=4(x+1) intersects the two distinct point. If m be the slope of the line I,, then
View Solution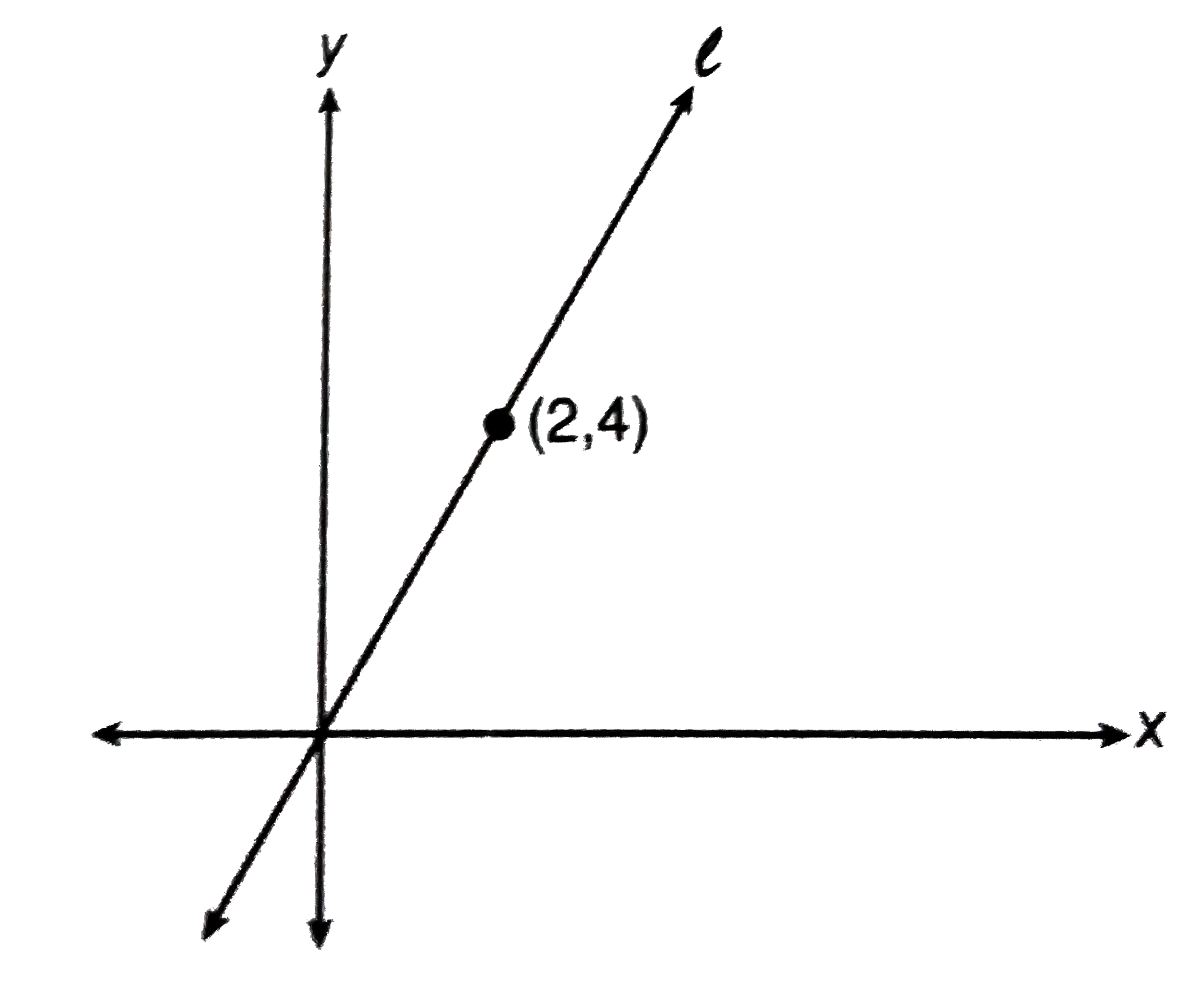
In the accompanying figure. Line l passes through the origin and the point (2, 4). Line m (not shown) is perpendicular to line l at (2, 4). Line m intersects the x-axis at which point?
View SolutionThe graph of line l in the xy-plane passes through the points (2,5)and(4,11). The graph of line m has a slope of -2 and an x-intercept of 2. If point (x, y) is the point of intersection of line l and m, what is the value of y?
View SolutionIf a line passes through the point of intersection of the lines 2x+y=5,x-y=1 and having slope 2 then it also passes through the point
View SolutionThe locus of point of intersection of any tangent to the parabola y2=4a(x−2) with a line perpendicular to it and passing through the focus, is
View SolutionLet P(2,4), Q(18, -12) be the points on the parabola y2=8x . The equation of straight line having slope 12 and passing through the point of intersection of the tangents to the parabola drawn at the points P and Q is
View Solution[" If two distinct chord of a parabola "y2=4ax" passing through the point "(a,2a)" are bisected by the line "x+y=1" then the length of the latus rectum cannot be
View Solution
