A line l passing through the origin is perpendicular to the lines
1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk−∞<t<∞and1_(2):(3+2s)ˆi+(3+2s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<s<∞
Then the coordinate(s) of the point(s) on 12 at a distance of √17 from the point of intersection of 1 and 11 is (are)
(73,73,53)
(−1,−1,0)
(1,1,1)
(79,79,89)
The correct Answer is:(b, d)
To solve the problem step by step, we will follow the outlined approach:
Step 1: Identify the direction ratios of the lines L1 and L2
The equations of the lines are given as:
- Line L1: (3+t)^i+(−1+2t)^j+(4+2t)^k
- Line L2: (3+2s)^i+(3+2s)^j+(2+s)^k
From these equations, we can extract the direction ratios:
- For L1, the direction ratios are ^d1=(1,2,2)
- For L2, the direction ratios are ^d2=(2,2,1)
Step 2: Find the direction ratios of line L
Since line L is perpendicular to both L1 and L2, we can find its direction ratios using the cross product of the direction ratios of L1 and L2.
^d1=(1,2,2),^d2=(2,2,1)
Calculating the cross product ^d1×^d2:
^dL=∣∣
∣
∣∣^i^j^k122221∣∣
∣
∣∣
Calculating the determinant:
^dL=^i(2⋅1−2⋅2)−^j(1⋅1−2⋅2)+^k(1⋅2−2⋅2)
=^i(2−4)−^j(1−4)+^k(2−4)
=−2^i+3^j−2^k
Thus, the direction ratios of line L are (−2,3,−2).
Step 3: Find the point of intersection of L and L1
Since line L passes through the origin, we can express it as:
Line L: (0,0,0)+λ(−2,3,−2)=(−2λ,3λ,−2λ)
To find the intersection with line L1, we equate the coordinates:
−2λ=3+t(1)
3λ=−1+2t(2)
−2λ=4+2t(3)
From equation (1):
t=−2λ−3
Substituting t into equation (2):
3λ=−1+2(−2λ−3)
3λ=−1−4λ−6
3λ+4λ=−7
7λ=−7⟹λ=−1
Now substituting λ=−1 back into the equations to find t:
t=−2(−1)−3=2−3=−1
Now substituting λ=−1 into the coordinates of L:
M=(−2(−1),3(−1),−2(−1))=(2,−3,2)
Step 4: Find the coordinates on L2 at a distance of √17 from point M
The distance formula between point M and a point on L2 (3+2s,3+2s,2+s) is given by:
√(3+2s−2)2+(3+2s+3)2+(2+s−2)2=√17
Squaring both sides:
(3+2s−2)2+(3+2s+3)2+(2+s−2)2=17
Simplifying:
(1+2s)2+(6+2s)2+(s)2=17
(1+4s+4s2)+(36+24s+4s2)+(s2)=17
9s2+28s+20=0
Step 5: Solve the quadratic equation
Using the quadratic formula s=−b±√b2−4ac2a:
s=−28±√282−4⋅9⋅202⋅9
s=−28±√784−72018
s=−28±√6418
s=−28±818
Calculating the two possible values for s:
1. s=−2018=−109
2. s=−3618=−2
Step 6: Find the coordinates for both values of s
For s=−2:
P=(3+2(−2),3+2(−2),2+(−2))=(3−4,3−4,0)=(−1,−1,0)
For s=−109:
P=(3+2(−109),3+2(−109),2−109)
=(3−209,3−209,2−109)
=(279−209,279−209,189−109)
=(79,79,89)
Final Answer
The coordinates of the points on L2 at a distance of √17 from the point of intersection of L and L1 are:
1. (−1,−1,0)
2. (79,79,89)
- Line L1: (3+t)^i+(−1+2t)^j+(4+2t)^k
- Line L2: (3+2s)^i+(3+2s)^j+(2+s)^k
- For L1, the direction ratios are ^d1=(1,2,2)
- For L2, the direction ratios are ^d2=(2,2,1)
∣
∣∣^i^j^k122221∣∣
∣
∣∣
=^i(2−4)−^j(1−4)+^k(2−4)
=−2^i+3^j−2^k
Line L: (0,0,0)+λ(−2,3,−2)=(−2λ,3λ,−2λ)
3λ=−1+2t(2)
−2λ=4+2t(3)
t=−2λ−3
3λ=−1+2(−2λ−3)
3λ=−1−4λ−6
3λ+4λ=−7
7λ=−7⟹λ=−1
t=−2(−1)−3=2−3=−1
M=(−2(−1),3(−1),−2(−1))=(2,−3,2)
(3+2s−2)2+(3+2s+3)2+(2+s−2)2=17
(1+2s)2+(6+2s)2+(s)2=17
(1+4s+4s2)+(36+24s+4s2)+(s2)=17
9s2+28s+20=0
s=−28±√282−4⋅9⋅202⋅9
s=−28±√784−72018
s=−28±√6418
s=−28±818
1. s=−2018=−109
2. s=−3618=−2
P=(3+2(−2),3+2(−2),2+(−2))=(3−4,3−4,0)=(−1,−1,0)
P=(3+2(−109),3+2(−109),2−109)
=(3−209,3−209,2−109)
=(279−209,279−209,189−109)
=(79,79,89)
1. (−1,−1,0)
2. (79,79,89)
Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 11 : Subjective Type Questions
1 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
35 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
A line l passing through the origin is perpendicular to the lines l1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk,−∞<t<∞, l2:(3+s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<t<∞ then the coordinates of the point on l2 at a distance of √17 from the point of intersection of l&l1 is/are:
View SolutionA line l passing through the origin is perpendicular to the lines l1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk,∞<t<∞,l2:(3+s)ˆi+(3+2s)ˆj+(2+s)ˆk,∞<t<∞ then the coordinates of the point on l2 at a distance of √17 from the point of intersection of l&l1 is/are:
View SolutionFind the equation of a line passing through the point (1,2,3) and perpendicular to the plane →r.(2ˆi−3ˆj+4ˆk)=1.
View SolutionThe vector →B=5ˆi+2ˆj−Sˆk is perpendicular to the vector →A=3ˆi+ˆj+2ˆk if S =
View SolutionThe unit vector perpendicular to the vectors 6ˆi+2ˆj+3ˆkand3ˆi−6ˆj−2ˆk, is
View SolutionThe vector →B=5ˆi+2ˆj−Sˆk is perpendicular to the vector →A=3ˆi+ˆj+2ˆk if S=
View SolutionFind the equation of the line which passes through the point (-1,3,-2) and is perpendicular to the lines x1=y2=z3 and →r=(−2ˆi+ˆj−ˆk)+λ(−3ˆi+2ˆj+5ˆk).
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
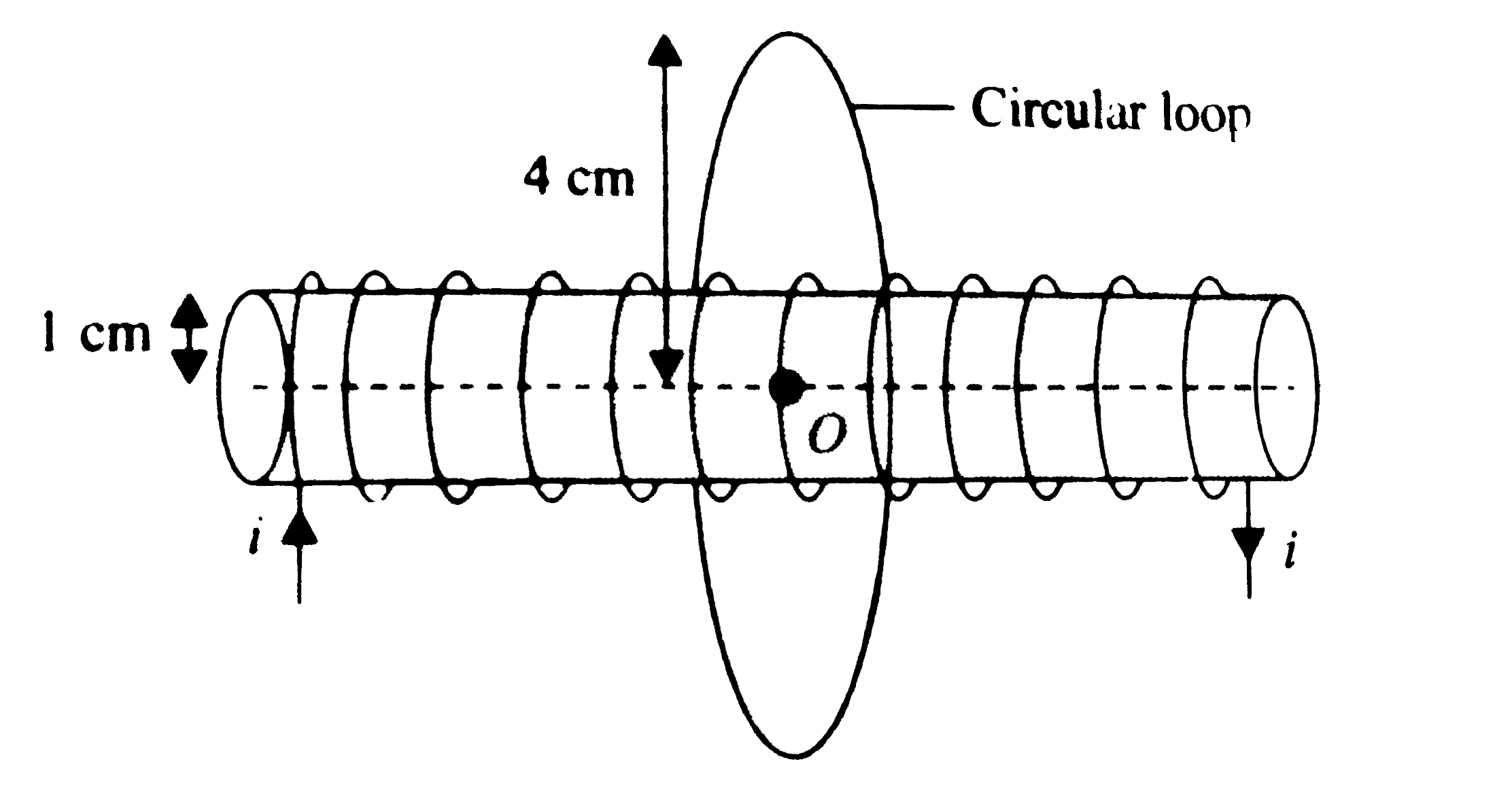
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionThe line →r=2ˆi−3ˆj−ˆk+λ(ˆi−ˆj+2ˆk) lies in the plane →r.(3ˆi+ˆj−ˆk)+2=0 or not
View SolutionEquation of a plane passing through the intersection of the planes →r.(3ˆi−ˆj+ˆk)=1 and →r.(ˆi+4ˆj−2ˆk)=2 and passing through the point (ˆi+2ˆj−ˆk) is :
View Solution
