A line segment AB is divided at point P such that PB : AB = 3:7, then the ratio of AP : PB = ________.
To solve the problem, we need to find the ratio of AP:PB given that PB:AB=3:7.
1. Understanding the Given Ratio:
We are given that PB:AB=3:7. This means that if we let PB=3x, then AB=7x for some value x.
2. Finding the Length of AP:
Since AB is the total length of the segment and can be expressed as the sum of AP and PB, we can write:
AB=AP+PB
Substituting the values we have:
7x=AP+3x
3. Rearranging the Equation:
To find AP, we can rearrange the equation:
AP=7x−3x
Simplifying this gives:
AP=4x
4. Finding the Ratio AP:PB:
Now we have AP=4x and PB=3x. We can now find the ratio:
AP:PB=4x:3x
Since x is common in both terms, we can simplify this to:
AP:PB=4:3
Thus, the ratio of AP:PB is 4:3.
Final Answer:
The ratio of AP:PB=4:3.
We are given that PB:AB=3:7. This means that if we let PB=3x, then AB=7x for some value x.
Since AB is the total length of the segment and can be expressed as the sum of AP and PB, we can write:
AB=AP+PB
Substituting the values we have:
7x=AP+3x
To find AP, we can rearrange the equation:
AP=7x−3x
Simplifying this gives:
AP=4x
Now we have AP=4x and PB=3x. We can now find the ratio:
AP:PB=4x:3x
Since x is common in both terms, we can simplify this to:
AP:PB=4:3
The ratio of AP:PB=4:3.
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - self assesment -1 (Very Short Answer Type Questions)
1 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - self assesment -1 (II. Short Answer Type Questions)
2 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - self assesment -1 (Objective Type Questions : ) A. Multiple Choice Questions
2 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SELF ASSESSMENT
5 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
Similar Questions
Fill in the blanks/tables with suitable information:
If a line segment AB of length 6 cm is divided internally by a point C in the ratio of 3:2, then the length of AC is ___________ .
View SolutionA line segment AB is 8 cm in length. AB is produced to P such that BP2=AB.AP, find the length of BP.
View Solution
Knowledge Check
A line segment AB of length 16 is divided into two part AP and PB by a point P .If AP2+PB2 is minimum, then
AP trisects seg ABBAP:PB=3:1CP bisects seg ABDAP:PB=1:3If point P(-4,6) divides the line segment AB with A(-6,10) in the
ratio 2:1 , then coordinates of the point B are _ _ _ _ _ _ _ _A(4,3)B(3,-4)C(3,4)D(-3,4)
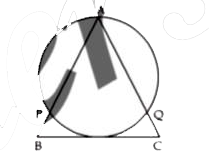
A circle is drown with diameter as the high of an equilateral triangles. As shown in the figure, the circle cuts side AB and AC at point P and Q. Find the ratio of AP : PB
View SolutionA line segment AB is divided internally and externally in the same ratio (>1) at PandQ respectively and M is mid point of AB. Statement-1: MP,MB,MQ are in G.P. Statement-2 AP,ABandAQ are in H.P.
View SolutionA line segment AB is divided internally and externally in the same ratio at P and Q respectively and M is the mid-point of AB. Statement I : MP, MB, MQ are in G.P. Statement II : AP, AB and AQ are in H.P.
View SolutionThe line segment AB is divided at P(1,1) internally in the ratio 5:2 and coordinates of point B are (−1,−1) find the coordinates of point A.
View SolutionDraw segment AB of length 4 cm. Divide it in ratio 2 : 3
View SolutionTo find a point P on the line segment AB = 6 cm, such that APAB=25, in which ratio the line segment AB is divided.
View Solution
