A man standing on the deck of a ship, which is 10m above water level. He observes the angle of elevation of the top of a hill as and the angle of depression of the base of the hill as Calculate the distance of the hill from the ship and the height of the hill.
Let the height of the hill AB = h m and let the position of man at 10 m above the sea-level is D.
Let
In right ,
tan30^(@)=(DC)/(BC) rArr 1/sqrt3=10/x rArr x=10sqrt3 m …(1)
Hence, the distance of the hill from the ship id x i.e., and height of the hill is 40 m.
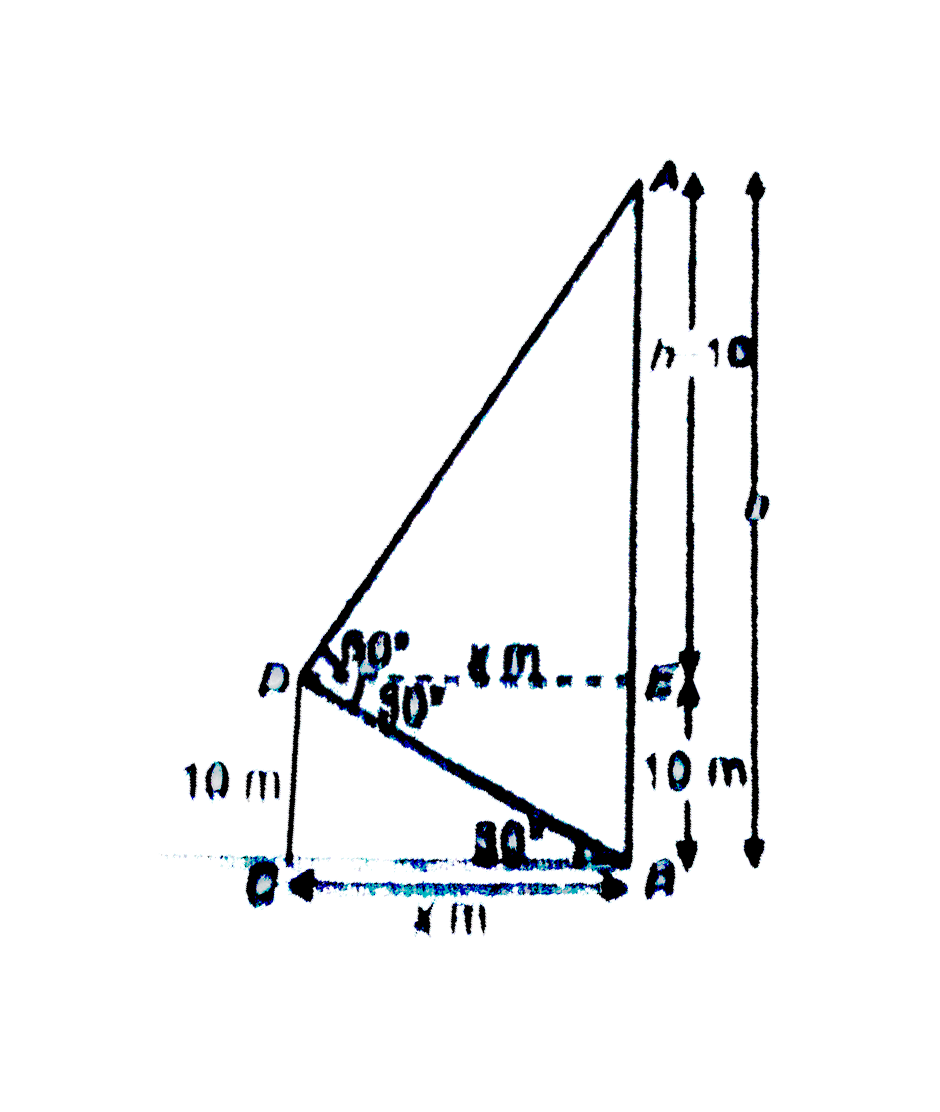
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Exercise
32 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)
5 Videos
- REAL NUMBERSBOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions
5 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
Similar Questions
A man standing on the deck of a ship, which is 10m above water level. He observes the angle of elevation of the top of a hill as 600 and the angle of depression of the base of the hill as 300. Calculate the distance of the hill from the ship and the height of the hill.
View SolutionA man is standing on the deck of a ship, which is 8m above water level. He observes the angle of elevation of the top of a hill as 60∘ and the angle of depression of the base of the hill as 30∘. Calculate the distance of the hill from the ship and the height of the hill
View Solution
Knowledge Check
From a point 12 m above the water level, the angle of elevation of the top of a hill is 60∘ and the angle of depression of the base of the hill is 30∘. What is the height (in m)of the hill?
A36B48√3C48D36√3The angle of elevation of the top of a hill from the foot of a tower is 60∘ and the angle of elevation of the top of the tower from the foot of the hill is 30∘. If the tower is 50 m high, then what is the height of the hill?
A100√3mB50√3mC150mD150√3m
A man standing on the deck of a ship, which is 8m above water level. He observes the angle of elevation of the top of a hill as 60o and the angle of depression of the base of the hill as 30o . Calculate the distance of the hill from the ship and the height of the hill.
View SolutionA man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60∘ and the angle of depression the base of hill as 30∘. Find the distance of the hill from the ship and the height of the hill.
View SolutionA man on the deck of a ship is 10m above the water level. He observes that the angle of elevation of the top of a cliff is 45o and the angle of depression of the base is 30o . Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionAman on deck of a ship is 12 m above the water level. He observes that the angle of the elevation of the top of a cliff is 45∘ and the angle of depression of its base is 30∘. Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionA man on the deck of a ship 12 m above water level, observes that the angle of elevation of the top of a cliff is 60∘ and the angle of depression of the base of the is 30∘. Find the distance of the cliff from the ship and the height of the cliff. [use √3=1.732)
View SolutionThe angle of elevation of the top of a hill at the foot of a tower is 60o and the angle of elevation of the top of the tower from the foot of the hill is 30o . If the tower is 50 m high, what is the height of the hill?
View Solution
