A milk container is 8cm long and 50cm wide. What should be its height so that it can hold 4 litres of milk?
To find the height of a milk container that is 8 cm long and 50 cm wide, which needs to hold 4 liters of milk, we can follow these steps:
1. Identify the dimensions of the cuboid:
- Length (L) = 8 cm
- Width (W) = 50 cm
- Height (H) = ? (to be determined)
2. Convert the volume from liters to cubic centimeters:
- We know that 1 liter = 1000 cm³.
- Therefore, 4 liters = 4 × 1000 cm³ = 4000 cm³.
3. Use the formula for the volume of a cuboid:
- The formula for the volume (V) of a cuboid is:
V=L×W×H
- Substituting the known values:
4000=8×50×H
4. Calculate the product of length and width:
- Calculate 8×50:
8×50=400
- Now, the equation becomes:
4000=400×H
5. Solve for height (H):
- Rearranging the equation to find H:
H=4000400
- Simplifying the fraction:
H=10 cm
6. Conclusion:
- The height of the milk container should be 10 cm.
Final Answer:
The height of the milk container is 10 cm.
---
- Length (L) = 8 cm
- Width (W) = 50 cm
- Height (H) = ? (to be determined)
- We know that 1 liter = 1000 cm³.
- Therefore, 4 liters = 4 × 1000 cm³ = 4000 cm³.
- The formula for the volume (V) of a cuboid is:
V=L×W×H
- Substituting the known values:
4000=8×50×H
- Calculate 8×50:
8×50=400
- Now, the equation becomes:
4000=400×H
- Rearranging the equation to find H:
H=4000400
- Simplifying the fraction:
H=10 cm
- The height of the milk container should be 10 cm.
The height of the milk container is 10 cm.
Topper's Solved these Questions
- MENSURATION-I (AREA OF A TRAPEZIUM AND A POLYGONBOOK - RD SHARMA ENGLISHCHAPTER - MENSURATION-I (AREA OF A TRAPEZIUM AND A POLYGONEXERCISE - All Questions
84 Videos
- MENSURATION-III (SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDER)BOOK - RD SHARMA ENGLISHCHAPTER - MENSURATION-III (SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDER)EXERCISE - All Questions
109 Videos
Similar Questions
Knowledge Check
A rectangle is 8cm long and 5cm wide. Its perimeter is doubled when each of its sides is increased by cm. Form an equation in x and find the new length of the rectangle.
A13.5cmB14.5cmC14.15cmD12.5cm
A staircase contains three steps each 10 cm high and 20 cm wide figure. What should be the minimum horizontal velocity of a bal rolling off the upper most plane so as to hit directly the lowest plane?
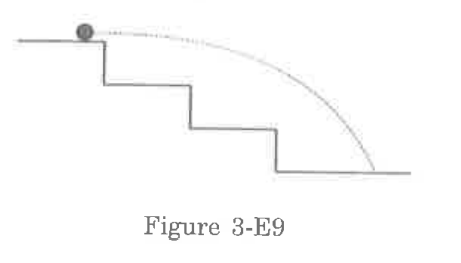
View SolutionA staircase contains three steps each 10 cm high and 20 cm wide figure. What should be the minimum horizontal velocity of a bal rolling off the upper most plane so as to hit directly the lowest plane?

View SolutionA staircase contains three steps each 10 cm high and 20 cm wide figure. What should be the minimum horizontal velocity of a bal rolling off the upper most plane so as to hit directly the lowest plane?

View SolutionA wire in the form of a rectangle 18.7 cm long and 14.3 cm wide is reshaped and bent into the form of a circle. Find the radius of the circle so formed.
View SolutionWater is flowing at the rate of 15km/hour through a pipe of diameter 14cm into a cuboidal pond which is 50m long and 44m wide. In what time will the level of water in the pond rise by 21cm?
View SolutionA milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of milk at the rate of ₹22 per L which the container can hold.
View SolutionA cuboidal water tank is 6m long, 5m wide and 4.5m deep. How many litres of water can it hold?
View Solution
