A parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
From the figure, it is clear that the length of the edges of the parallelepiped a,b,c is x2−x1,y2−y1,z2−z1 or 6−3,8−4and10−8or3,4and2. Therefore,
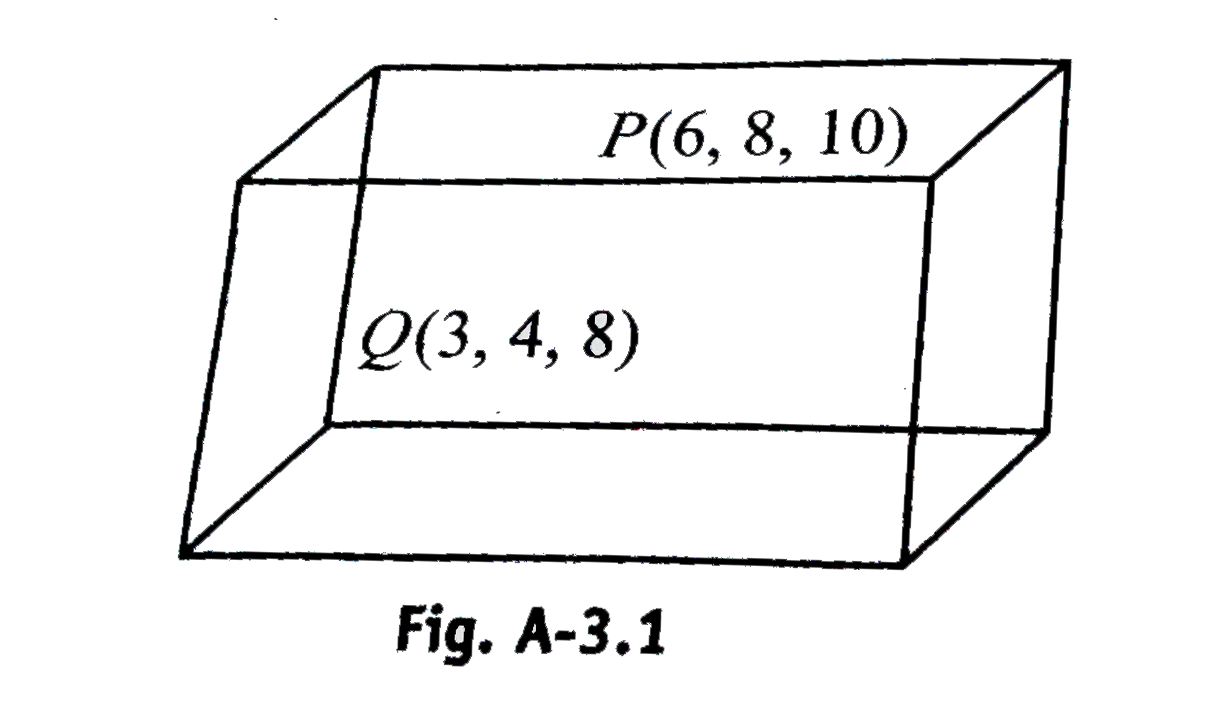
The length of the diagonal will be
√a2+b2+c2=√9+16+4=√39.
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.2
15 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.3
19 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - JEE Previous Year
26 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
34 Videos
Similar Questions
A parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
View SolutionA parallelepiped is formed by planes drawn through the points P(6, 8, 10) and Q(3, 4, 8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallolepiped.
View Solution
Knowledge Check
A parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
A2√3B3√2C√2D√3If a parallelopiped is formed by planes drawn through the points (5,8,10) and (3,6,8) parallel to the coordinate planes, then the length of diagonal of the parallelopiped is
A2√3B3√2C√2D√3If a parallelopiped is formed by planes drawn
through the points (2, 5, 3) and (6, 7, 9) parallel to
the coordinate planes, then the length of its
diagonal isA2√3B3√2C√2D√3
A parallelepiped is formed by planes drawn through the points (2,3,5)and(5,9,7) , parallel to the coordinate planes. The length of a diagonal of the parallelepiped is a.7 unit b. √38 unit c. √155 unit d. none of these
View SolutionA rectangular parallelopiped is formed by drawing planes through the points (1,2,5)and(−1,−1,−1) parallel to the coordinate planes. Find the length of the diagnol of the parallelopiped.
View SolutionAparallelopiped is formed by planes drawn through the points (2,3,5)and(5,9,7) parallel to the coordinate planes. The length of the diagonal of the parallelopiped is ……
View SolutionA parallelopiped is formed by planes drawn through the point (2,2,5) and (5,9,7) parallel to the coordinte planes. The length of a diagonal of the parallelopiped is (A) 7 (B) 9 (C) 11 (D) √155
View SolutionA rectangular parallelopiped is formed by planes drawn through the points (5,7,9) and (2,3,7) parallel to the coordinate planes. The length of an edge of this rectangular parallelopiped is
View Solution