A parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.Solution in Tamil
From the figure, it is clear that the length of the edges of the parallelepiped a,b,c is x2−x1,y2−y1,z2−z1 or 6−3,8−4and10−8or3,4and2. Therefore,
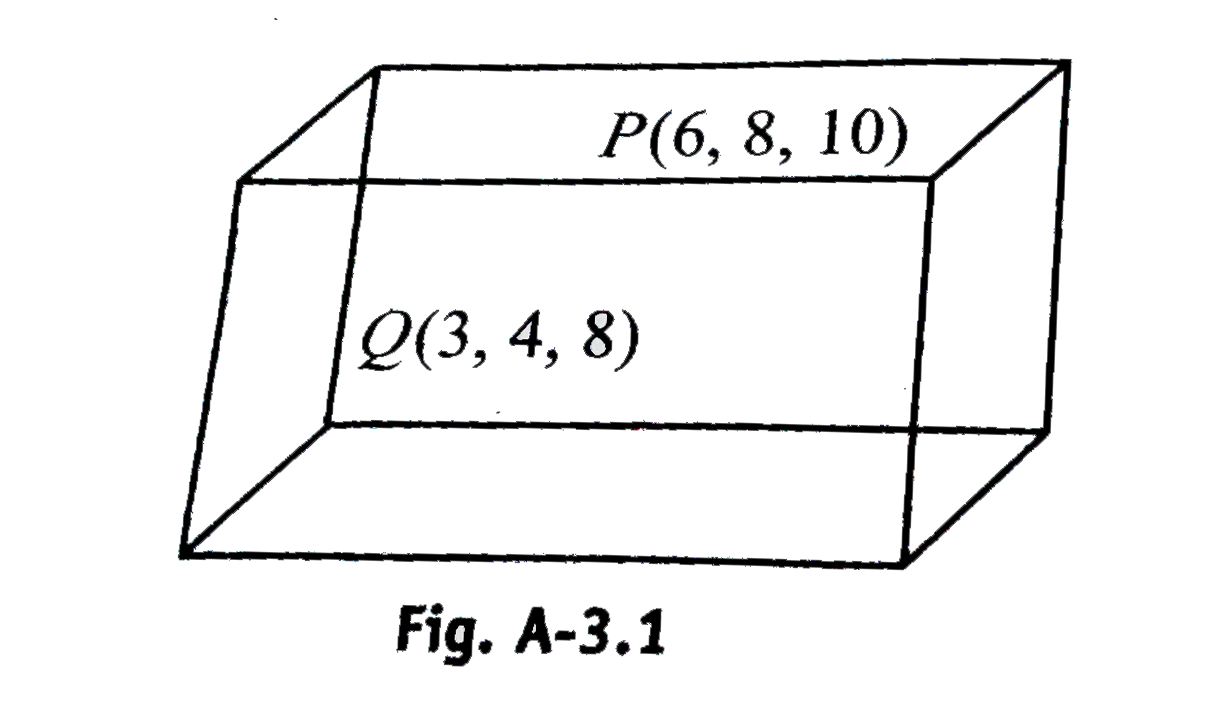
The length of the diagonal will be
√a2+b2+c2=√9+16+4=√39.
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.2
15 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.3
19 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - JEE Previous Year
26 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
12 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
4 Videos
Similar Questions
Find the point where line which passes through point (1,2,3) and is paralle to line →r=ˆi+ˆj+2ˆk+λ(ˆi−2ˆj+3ˆk) meets the xy-plane.
View SolutionFind the angle between the line x−13=y−12=z−14 and the plane 2x+y−3z+4=0.
View Solution(i) Find the equation of the plane passing through the points(2,1,0),(5,0,1)and(4,11). (ii) If P s the point (2,1,6), then the find the point Q such that PQ is perpendicular to the plane in (i) and the midpoint of PQ lies on it.
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionThe number of solution (s) of the equation
√2+cos2x=(sinx+cosx)∈[−π2,π]
View SolutionA parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
View SolutionA parallelepiped is formed by planes drawn through the points (2,3,5)and(5,9,7) , parallel to the coordinate planes. The length of a diagonal of the parallelepiped is a.7 unit b. √38 unit c. √155 unit d. none of these
View SolutionA parallelepiped is formed by planes drawn through the points P(6,8,10) and Q(3,4,8) parallel to the coordinate planes.Find the length of edges and diagonal of the parallolepiped.
View SolutionPlanes r drawn parallel to the coordinate planes through the point P(x1,y1, z1) and Q(x2,y2,z2) . Find the length of the edges of the parallelepiped so formed.
View SolutionPlanes are drawn parallel to the coordinate planes through the points (3,0,-1) and (-2,5,4). Find the lengths of the edges of he parallelepiped so formed.
View SolutionIf a parallelepiped is formed by the planes drawn through the points (2,3,50 and (5,9,7) parallel to the coordinate planes, then write the lengths of edges of the parallelopiped and length of the diagonal.
View SolutionA parallelepiped is formed by planes drawn parallel to coordinate axes through the points A=(1,2,3) and B=(9,8,5). The volume of that parallelepiped is equal to (in cubic units)
View SolutionFind the lengths of the edges of the rectangular parallelepiped formed by planes drawn throgh points (1,2,3) and (4,7,6) parallel to the co ordinate planes
View SolutionA parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
View SolutionA parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
View SolutionA parallelepiped is formed by planes drawn parallel to coordinate axes through the points A=(1,2,3) and B=(9,8,5). The volume of that parallelepiped is equal to (in cubic units)
View Solution
