A park, in the shape of a quadrilateral has . How much area does it occupy?
To find the area of the quadrilateral park ABCD, we can divide it into two triangles: triangle BCD and triangle ABD.
Step 1: Calculate the area of triangle BCD
Since angle C is 90 degrees, we can use the formula for the area of a right triangle:
AreaBCD=12×base×height
Here, we can take BC as the height and CD as the base.
AreaBCD=12×BC×CD=12×12m×5m=12×60=30m2
Step 2: Find the length of BD using the Pythagorean theorem
In triangle BCD, we can find BD using the Pythagorean theorem:
BD2=BC2+CD2
Substituting the known values:
BD2=122+52=144+25=169
Taking the square root:
BD=√169=13m
Step 3: Calculate the area of triangle ABD using Heron's formula
First, we need to calculate the semi-perimeter (s) of triangle ABD:
s=AB+AD+BD2=9+8+132=302=15m
Now, we can use Heron's formula to find the area of triangle ABD:
AreaABD=√s(s−AB)(s−AD)(s−BD)
Substituting the values:
AreaABD=√15(15−9)(15−8)(15−13)=√15×6×7×2
Calculating the product:
=√15×6×7×2=√1260
To simplify √1260:
1260=22×32×5×7
√1260=6√35≈6×5.916=35.496m2
Step 4: Calculate the total area of quadrilateral ABCD
Now, we can find the total area of quadrilateral ABCD by adding the areas of triangles BCD and ABD:
AreaABCD=AreaBCD+AreaABD=30m2+35.496m2≈65.496m2
Final Answer
The area of the park ABCD is approximately 65.496m2.
---
Since angle C is 90 degrees, we can use the formula for the area of a right triangle:
In triangle BCD, we can find BD using the Pythagorean theorem:
First, we need to calculate the semi-perimeter (s) of triangle ABD:
√1260=6√35≈6×5.916=35.496m2
Now, we can find the total area of quadrilateral ABCD by adding the areas of triangles BCD and ABD:
The area of the park ABCD is approximately 65.496m2.
Topper's Solved these Questions
- HERONS FORMULABOOK - NCERTCHAPTER - HERONS FORMULAEXERCISE - Exercise 12.1
6 Videos
- HERONS FORMULABOOK - NCERTCHAPTER - HERONS FORMULAEXERCISE - Solved Examples
6 Videos
- COORDINATE GEOMETRYBOOK - NCERTCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.2
2 Videos
- INTRODUCTION TO EUCLIDS GEOMETRYBOOK - NCERTCHAPTER - INTRODUCTION TO EUCLIDS GEOMETRYEXERCISE - Solved Examples
3 Videos
Similar Questions
A park, in the shape of a quadrilateral ABCD, has ∠C=90∘, AB=9cm, BC=12cm, CD=5m and AD=8m. How much area does it occupy? So, we can calculate BD by applying Pythagoras theorem
View SolutionA park in the shape of a quadrilateral ABCD has∠C=90∘,AB=9m,BC=12m,CD=5m and AD=8m How much area does it occupy
View Solution
Knowledge Check
In a cyclic quadrilateral ABCD∠A+∠B+∠C+∠D=?
AA)90∘BB)360∘CC)180∘DD)120∘
A park, in the shape of a quadrilateral ABCD, has ∠C=90o, AB=9m, BC=12m, CD=5mand AD=8m. How much area does it occupy?
View SolutionABCD is a quadrilateral with ∠C=90degree. AB=9,AD=8, BC=12, CD=5. Find area of ABCD
View SolutionCalculate the area of the quadrilateral ABCD as shown in Fig.33, given that BD=42 cm , AC=28 cm , OD=12 cm and AC⊥BD .
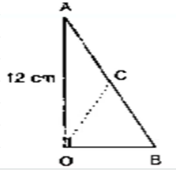
View SolutionIn Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
View SolutionIn Fig. 10.57, a circle is inscribed in a quadrilateral ABCD in which ∠B=90o . If AD=23cm , AB=29cm and DS=5cm , find the radius r of the circle. (FIGURE)
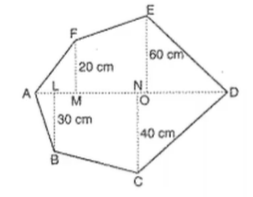
View SolutionFind the area of the following polygon, if AL=10cm, AM=20cm, AN=50cm, AO=60cm and AD=90cm.
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View Solution
