A park is in the shape of quadrilateral ABCD in which and . Find the area of the park.
The correct Answer is:A
To find the area of the park shaped as quadrilateral ABCD, we can divide it into two triangles: triangle BCD and triangle ABD. Given the dimensions and angle, we can use the following steps:
Step 1: Identify the triangles
We have quadrilateral ABCD with:
- AB = 9 cm
- BC = 12 cm
- CD = 5 cm
- AD = 8 cm
- Angle C = 90°
We can divide the quadrilateral into two triangles: triangle BCD and triangle ABD.
Step 2: Calculate the area of triangle BCD
Triangle BCD is a right triangle (since angle C is 90°). The area of a right triangle can be calculated using the formula:
Area=12×base×height
Here, we can take CD as the base and BC as the height:
Area of △BCD=12×CD×BC=12×5×12=602=30 cm2
Step 3: Calculate the length of diagonal BD using Pythagoras theorem
In triangle BCD:
BD2=BC2+CD2
Substituting the values:
BD2=122+52=144+25=169
Taking the square root:
BD=√169=13 cm
Step 4: Calculate the area of triangle ABD using Heron's formula
First, we need to find the semi-perimeter (s) of triangle ABD:
s=AB+AD+BD2=9+8+132=302=15 cm
Now, we can use Heron's formula to find the area:
Area=√s(s−AB)(s−AD)(s−BD)
Substituting the values:
Area=√15(15−9)(15−8)(15−13)=√15×6×7×2
Calculating inside the square root:
=√15×6×7×2=√1260
Breaking it down:
=√15×6×14=√15×84=√1260
Calculating further:
=6√35 cm2
Step 5: Calculate the total area of the park
Now, we add the areas of triangles BCD and ABD:
Total Area=Area of △BCD+Area of △ABD=30+6√35 cm2
Step 6: Approximate the area
Using the approximate value of √35≈5.91:
6√35≈6×5.91≈35.46
Thus,
Total Area≈30+35.46=65.46 cm2
Final Answer
The area of the park is approximately 65.46 cm2.
---
We have quadrilateral ABCD with:
- AB = 9 cm
- BC = 12 cm
- CD = 5 cm
- AD = 8 cm
- Angle C = 90°
Triangle BCD is a right triangle (since angle C is 90°). The area of a right triangle can be calculated using the formula:
Area=12×base×height
Here, we can take CD as the base and BC as the height:
Area of △BCD=12×CD×BC=12×5×12=602=30 cm2
In triangle BCD:
BD2=BC2+CD2
Substituting the values:
BD2=122+52=144+25=169
Taking the square root:
BD=√169=13 cm
First, we need to find the semi-perimeter (s) of triangle ABD:
s=AB+AD+BD2=9+8+132=302=15 cm
Now, we can use Heron's formula to find the area:
Area=√s(s−AB)(s−AD)(s−BD)
Substituting the values:
Area=√15(15−9)(15−8)(15−13)=√15×6×7×2
Calculating inside the square root:
=√15×6×7×2=√1260
Breaking it down:
=√15×6×14=√15×84=√1260
Calculating further:
=6√35 cm2
Now, we add the areas of triangles BCD and ABD:
Total Area=Area of △BCD+Area of △ABD=30+6√35 cm2
Using the approximate value of √35≈5.91:
6√35≈6×5.91≈35.46
Thus,
Total Area≈30+35.46=65.46 cm2
The area of the park is approximately 65.46 cm2.
Topper's Solved these Questions
- HERONS'S FORMULABOOK - NAGEEN PRAKASHANCHAPTER - HERONS'S FORMULAEXERCISE - Exercise 12b
10 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - EXAMPLE SOLUTION.
19 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise
3 Videos
Similar Questions
Knowledge Check
The base of a right prism is a quadrilateral ABCD. Given that AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm and ∠DAB=90∘. If the volume of the prism be 2070cm3, then the area of the lateral surface is
A720cm2B810cm2C1260cm2D2070cm2
Find the area of the quadrilateral ABCD in which AB=3cm,BC=4cm,CD=4cm,DA=5cm and AC=5cm.
View SolutionConstruct a quadrilateral ABCD with AB = 4 cm, BC = 2.8 cm, CD = 4 cm, ∠B=75∘and∠C=105∘
View SolutionFind the area of the quadrilateral ABCD, in which AB=7cm, BC=6cm, CD=12 cm, DA=15cm and AC=9 cm.
View SolutionFind the area of the quadrilateral ABCD , in which AB=7cm,BC=6cm,CD=12cm,DA=15cmandAC=9cm
View SolutionFind the area of a quadrilateral ABCD is which AB=3cm, BC=4cm, CD=4cm, DA=5cm and AC=5cm
S=12(a+b+c)=12(3+4+5)=6
arof ABC=sqrt(s(s-a)(s-b)(s-c)<br>ar ABC=√6(6−3)(6−4)(6−5)
⇒√6×3×2×1=6cm2
Now in △ADC,S=a+b+c2
⇒s=5+4+52=142=7cm
By using Heron’s formula
Area of △ADC=√s(s−a)(s−b)(s−c)
=√7(7−5)(7−4)(7−5)
=√7×2×3×2
=2√21cm2
Area of△ADC=9.2cm2 (approx.)
Area of the quadrilateral ABCD = Area of △ADC+Areaof△ABC=9.2cm2+6cm2=15.2cm2
Thus, the area of the quadrilateral,ABCDis15.2cm2.
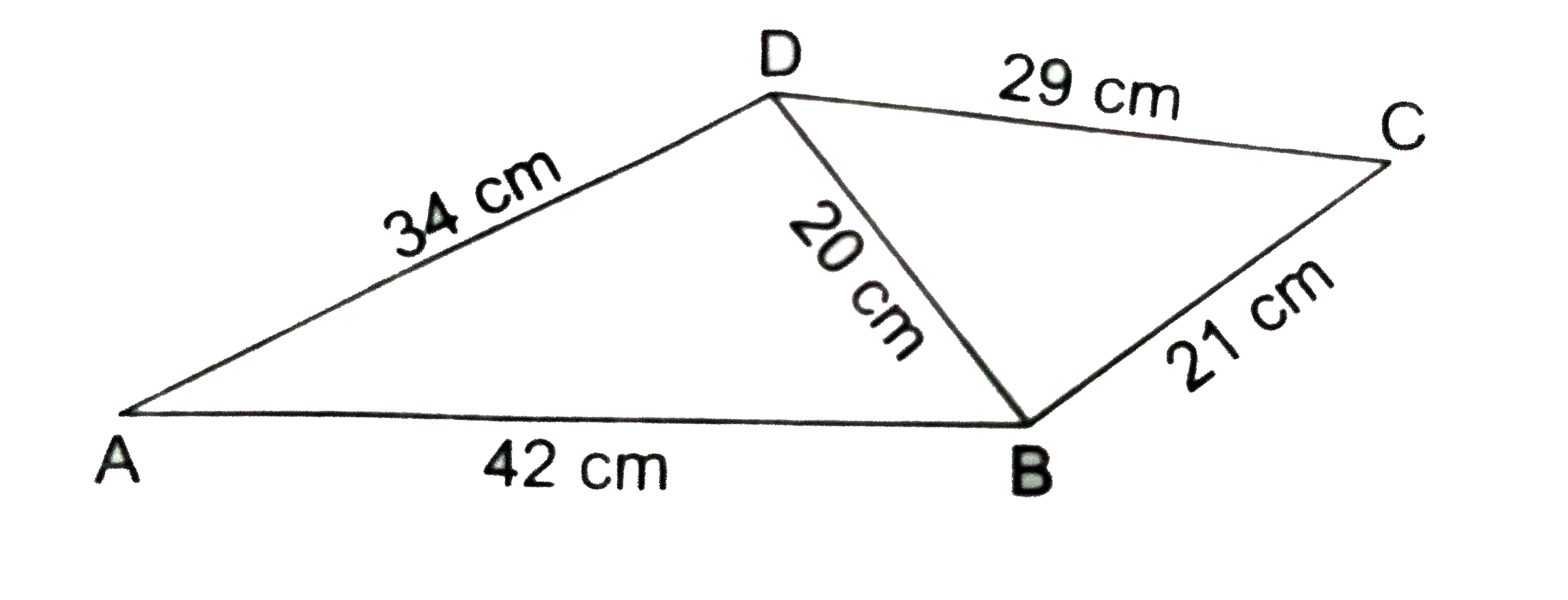
View SolutionFind the area of the quadrilateral ABCD in which AB= 42 cm. Bc=21cm,CD=29cm,DA=34cmand diagonal BD= 20 cm .
View SolutionIn a quadrilateral ABCD , AB = 5 cm , BC = 37 cm , CD = 35 cm , BD = 12 cm , and AD = 13 cm . Find its area .
View Solution