A particle moves in a straight line so that s=√t, then its acceleration is proportional to
(velocity)3
velocity
(velocity)2
(velocity)3/2
The correct Answer is:A
To solve the problem step by step, we start with the given position function of the particle:
Step 1: Write down the position function
The position of the particle is given by:
s=√t
Step 2: Differentiate to find velocity
To find the velocity v, we differentiate the position function s with respect to time t:
v=dsdt=ddt(√t)
Using the power rule, we can rewrite √t as t1/2:
v=12t−1/2=12√t
Step 3: Differentiate to find acceleration
Next, we differentiate the velocity function v to find the acceleration a:
a=dvdt=ddt(12√t)
Using the power rule again:
a=12⋅(−12)t−3/2=−14t−3/2
Step 4: Determine proportionality
From the expression for acceleration, we see that:
a=−14t−3/2
This indicates that the acceleration a is proportional to t−3/2.
Final Answer
Thus, the acceleration of the particle is proportional to t−3/2.
---
The position of the particle is given by:
s=√t
To find the velocity v, we differentiate the position function s with respect to time t:
v=dsdt=ddt(√t)
Using the power rule, we can rewrite √t as t1/2:
v=12t−1/2=12√t
Next, we differentiate the velocity function v to find the acceleration a:
a=dvdt=ddt(12√t)
Using the power rule again:
a=12⋅(−12)t−3/2=−14t−3/2
From the expression for acceleration, we see that:
a=−14t−3/2
This indicates that the acceleration a is proportional to t−3/2.
Thus, the acceleration of the particle is proportional to t−3/2.
Topper's Solved these Questions
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Section I - Solved Mcqs
27 Videos
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 2
60 Videos
- DIFFERENTIAL EQUATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
A particle is moving in a straight line with uniform velocity. Its acceleration is
ApositiveBnegativeCzeroDnone of theseA particle is moving in a straight line with uniform velocity. Its acceleration is
ApositiveBnegativeCzeroDnone of theseA particle is moving on a straight line such that square of its velocity is directly proportional to distance as shown in graph. What is the acceleration of the particle ?
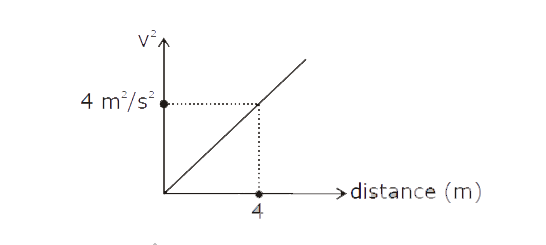 A14m/s2B1m/s2C2m/s2D12m/s2
A14m/s2B1m/s2C2m/s2D12m/s2
The displacement 'x' and time of travel 't' for a particle moving an a straight line are related as t=√(x+1)(x−1). Its acceleration at a time t is
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View Solution
