A person on a ship sailing north sees two lighthouses which are 6 km apart, in a line due west . After an hour's tailing one of them bears south west and the other southern south west. The ship is travelling at a rate of
12 km/hr
6 km/hr
3√2 km/hr
(6+3√2) km/hr
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Understand the problem and set up the diagram
We have two lighthouses, A and B, which are 6 km apart in a line due west. The ship is initially sailing north and after one hour, the lighthouses are seen at angles of south-west and south-south-west respectively.
Step 2: Define the positions
- Let the position of the first lighthouse (A) be at point (0, 0).
- The position of the second lighthouse (B) will then be at point (-6, 0) since they are 6 km apart in a line due west.
- Let the position of the ship after one hour be point C.
Step 3: Determine the angles
- The angle from the ship to lighthouse A (south-west) is 45 degrees.
- The angle from the ship to lighthouse B (south-south-west) is 22.5 degrees.
Step 4: Set up the triangle
Using the angles and the distance between the lighthouses, we can set up the triangle ADB where:
- A is the position of lighthouse A
- B is the position of lighthouse B
- D is the position of the ship after one hour (point C)
Step 5: Use trigonometry to find distances
Using the tangent function:
- For triangle ACD (where D is the position of the ship after one hour):
tan(45∘)=ADCD
Since tan(45∘)=1, we have:
AD=CD
- For triangle BCD:
tan(22.5∘)=BDCD
Rearranging gives us:
BD=CD⋅tan(22.5∘)
Step 6: Calculate distances
Since the distance between A and B is 6 km:
AB=AD+BD=6
Substituting the expressions we derived:
CD+CD⋅tan(22.5∘)=6
CD(1+tan(22.5∘))=6
Thus:
CD=61+tan(22.5∘)
Step 7: Calculate the speed of the ship
Since the ship traveled for one hour, the speed of the ship is equal to the distance traveled:
Speed=CD
Substituting the value of CD:
Speed=61+tan(22.5∘)
Step 8: Final calculation
Using the known value of tan(22.5∘)=√2−1:
Speed=61+(√2−1)=6√2=6√2/2=3√2 km/h
Conclusion
The speed of the ship is 3√2 km/h.
---
We have two lighthouses, A and B, which are 6 km apart in a line due west. The ship is initially sailing north and after one hour, the lighthouses are seen at angles of south-west and south-south-west respectively.
- Let the position of the first lighthouse (A) be at point (0, 0).
- The position of the second lighthouse (B) will then be at point (-6, 0) since they are 6 km apart in a line due west.
- Let the position of the ship after one hour be point C.
- The angle from the ship to lighthouse A (south-west) is 45 degrees.
- The angle from the ship to lighthouse B (south-south-west) is 22.5 degrees.
Using the angles and the distance between the lighthouses, we can set up the triangle ADB where:
- A is the position of lighthouse A
- B is the position of lighthouse B
- D is the position of the ship after one hour (point C)
Using the tangent function:
- For triangle ACD (where D is the position of the ship after one hour):
tan(45∘)=ADCD
Since tan(45∘)=1, we have:
AD=CD
tan(22.5∘)=BDCD
Rearranging gives us:
BD=CD⋅tan(22.5∘)
Since the distance between A and B is 6 km:
AB=AD+BD=6
Substituting the expressions we derived:
CD+CD⋅tan(22.5∘)=6
CD(1+tan(22.5∘))=6
Thus:
CD=61+tan(22.5∘)
Since the ship traveled for one hour, the speed of the ship is equal to the distance traveled:
Speed=CD
Substituting the value of CD:
Speed=61+tan(22.5∘)
Using the known value of tan(22.5∘)=√2−1:
Speed=61+(√2−1)=6√2=6√2/2=3√2 km/h
The speed of the ship is 3√2 km/h.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - OBJECTIVE RD SHARMACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise
45 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
- INCREASING AND DECREASING FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - INCREASING AND DECREASING FUNCTIONSEXERCISE - Chapter Test
20 Videos
Similar Questions
Draw the lines of force due to two bar magnets, north pole of one facing the south pole of the other.
View SolutionTwo ships are 10km apart on a line joining south to north. The one farther north is steaming west at 20kmh−1. The other is steaming north at 20kmh−1. What their distance of closest approach ? How long do they take to reach itb ?
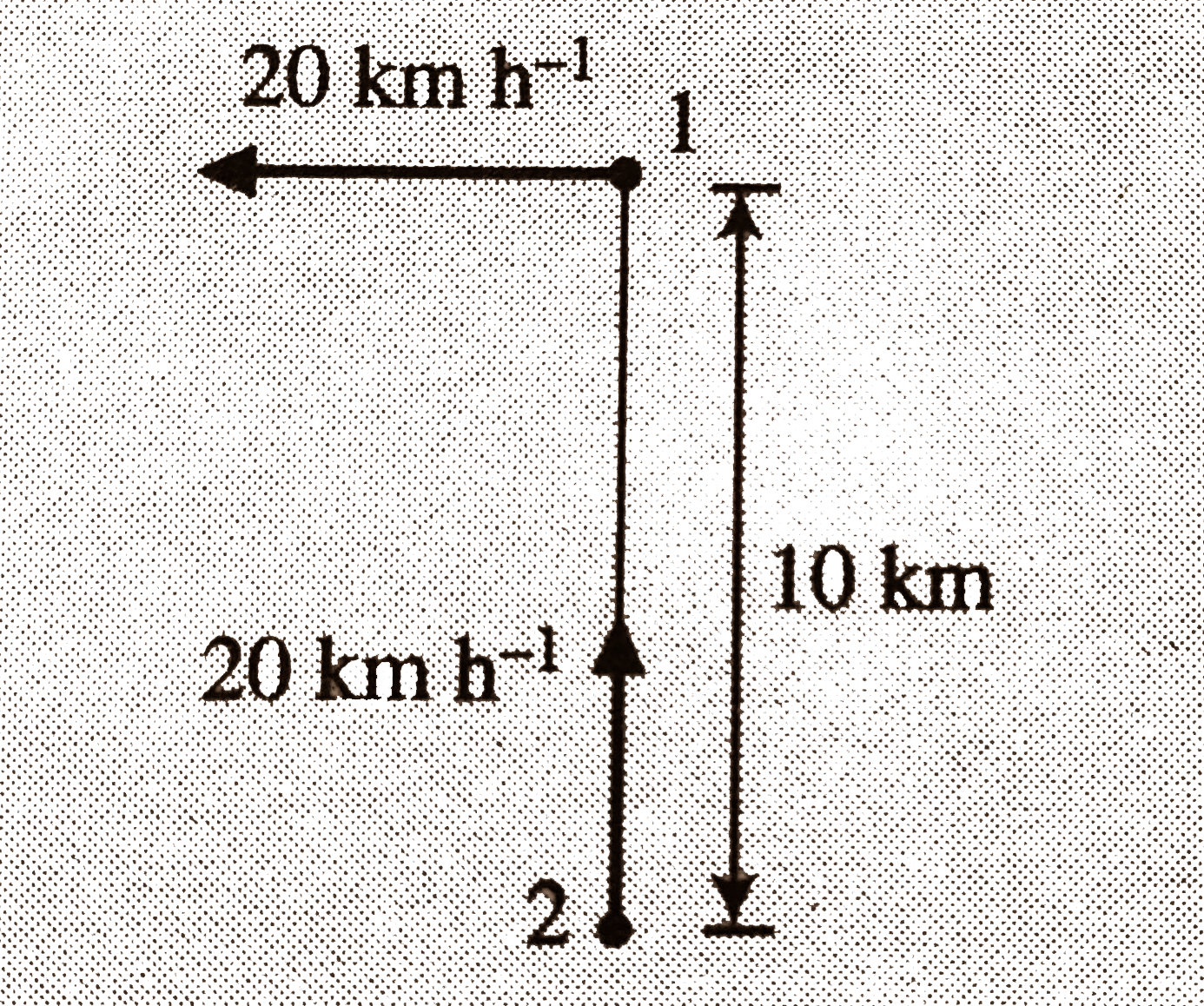 .
.
View Solution
Knowledge Check
Two ships are 10√2 km apart on a line running south to north. The one further north is moving west with a speed of 25 km/h, while the other towards north with a speed of 25 km/h.
ATheir distance of closest approach is 5√2 km.BTheir distance of closest approach is 10 kmCTime required to reach the closest distance is 17 minDTime required to reach the closest distance is 29 min.Two forces are applied to a 5.0 kg crate, one is 6.0N to the north and the other is 8.0N to the west. The magnitude of the acceleration of the crate is :
A0.50m/s2B2.0m/s2C2.8m/s2D10m/s2Two ships are 10km apart on a line from south to north.The one farther north is moving towards west at 40kmph and the other is moving towards north at 40kmph.Then distance of their closest approach is
A10kmB10√2kmC10√2kmD20km
Ship A is moving towards south with speed 3m/s and ship B is travelling due west with speed 4m/s Find the velocity of ship B with respect to ship A
View SolutionTwo ladies and two men are playing cards and are seated at North, East, South and West of a table, No lady is facing East. Persons sitting opposite each other are not of the same sex. One man is facing south. Which directions are the ladies facing ?
1) South and East
2) North and East
3) North and West
4) East and West
5) Data inadequate
View SolutionWhich one of the folloiwng climates is found in coastal areas of California in north America, Central Chile in South America and South - west ti of west Australia
View SolutionB is to the south-west of A. C is to the east of B and south-east of A and D is to the north of C in line with BA. In which direction of A is D located?
View SolutionK is a place which is located 2 km away in the north-west direction from the capital P. R is another place that is located 2 km away in the south-west direction from K. M is another place and that is located 2 km away in the north-west direction from R. T is yet another place that is located 2 km away in the south-west direction from M. In which direction is T located in relation to P?
View Solution
