A point moves so that the distance between the foot of perpendiculars from it on the lines ax2+2hxy+by2=0 is a constant 2d . Show that the equation to its locus is (x2+y2)(h2−ab)=d2{(a−b)2+4h2}.
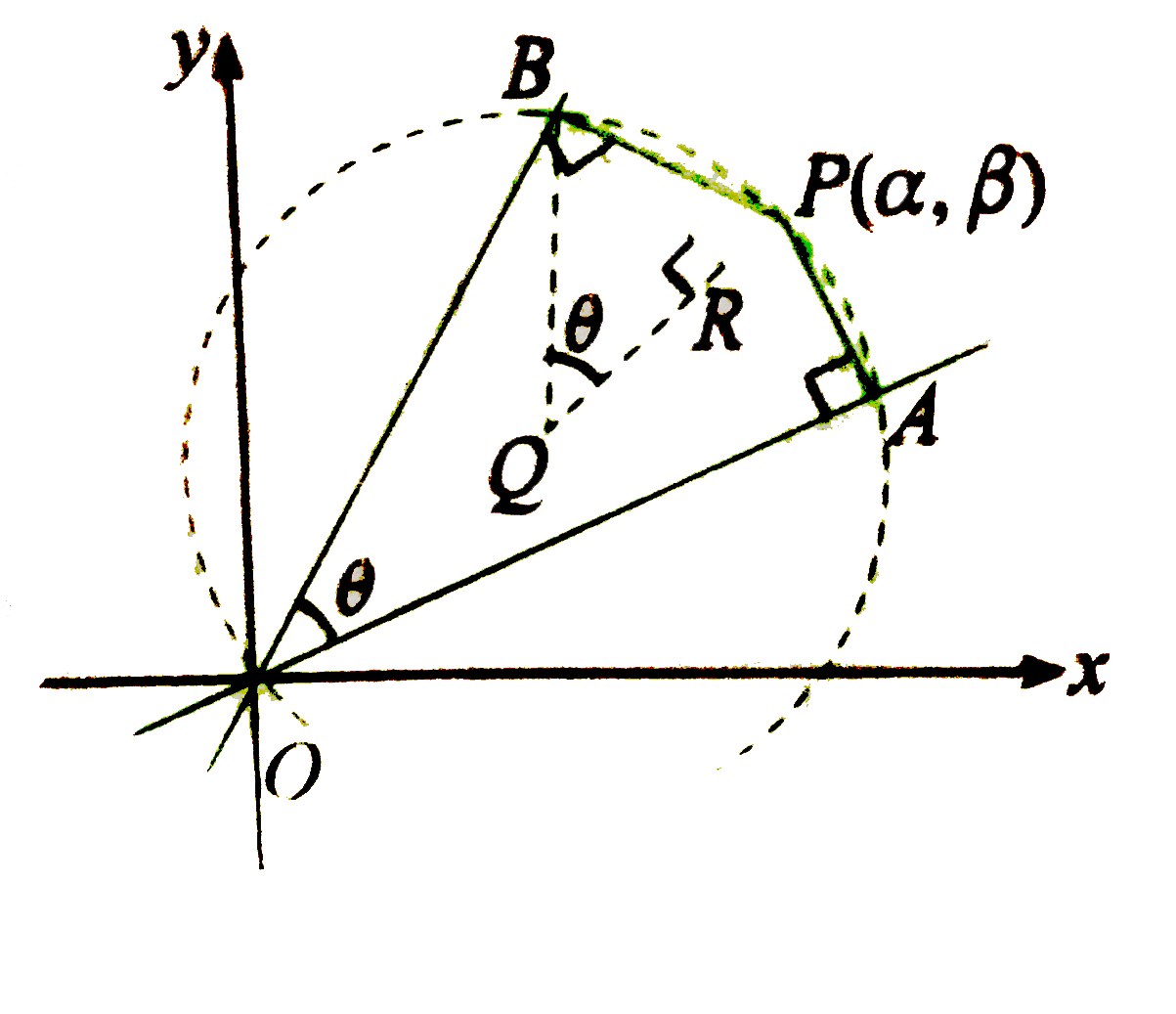
From point p(α,β), perpendiculars are dropped on the given pair of lines.
According to the question , AB=2d. Clearly OAPB is a cyclic quadrilateral and OP will be the diameter of the circumcircle of this quadrilateral.
OP=√α2+β2
Let Q be the center of the circle.
therefore , in ΔQRB,
sinθ=BRQB=2d√α2+β2 (1)
Also , angle between the lines is
tanθ=2√h2−ba+b (2)
Therefore , from (1) and (2), we get
2√h2−aba+b=2d√α2+β2−4d2
Therefore , the locus of P(α,β)is
(x2+y2)(h2−ab)=d2{(a−b)24h2}
Topper's Solved these Questions
- PAIR OF STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise 3.1
6 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise 3.2
7 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Illustration 3.17
1 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Matching Column Type
1 Videos
Similar Questions
A point moves so that the sum of its distances from (ae,0)and(−ae,0) is 2a, prove that the equation to its locus is x2a2+y2b2=1 , where b2=a2(1−e2).
View SolutionA point moves so that the sum of its distances from (ae,0)and(−ae,0) is 2a, prove that the equation to its locus is x2a2+y2b2=1 , where b2=a2(1−e2).
View SolutionShow that the locus of the foot of the perpendicular drawn from focus to a tangent to the hyperbola x2a2−y2b2=1 is x2+y2=a2.
View SolutionShow that the locus of the foot of the perpendicular drawn from focus to a tangent to the hyperbola x2a2−y2b2=1 is x2+y2=a2.
View SolutionProve that the product of the perpendiculars from (α,β) to the pair of lines ax2+2hxy+by2=0 is aα2+2hαβ+bβ2√(a−b)2+4h2
View SolutionProve that the product of the perpendiculars from (α,β) to the pair of lines ax2+2hxy+by2=0 is aα2+2hαβ+bβ2√(a−b)2+4h2
View SolutionThe straight lines joining any point P on the parabola y2=4ax to the vertex and perpendicular from the focus to the tangent at P intersect at R. Then the equation of the locus of R is
(a)x2+2y2−ax=0 (b)2x2+y2−2ax=0 (c)2x2+2y2−ay=0 (d) 2x2+y2−2ay=0
View SolutionFind the locus of the feet of the perpendiculars drawn from the point (b, 0) on tangents to the circle x2+y2=a2
View SolutionProve that the product of the perpendiculars from (α,β) to the pair of lines ax2+2hxy+by2=0 is aα2−2hαβ+η2√(a−b)2+4h2
View SolutionThe locus of the foot of the perpendicular from the foci an any tangent to the ellipse x2a2+y2b2=1, is
View Solution
