A point moves so that the distance between the foot of perpendiculars from it on the lines is a constant . Show that the equation to its locus is Solution in Bengali
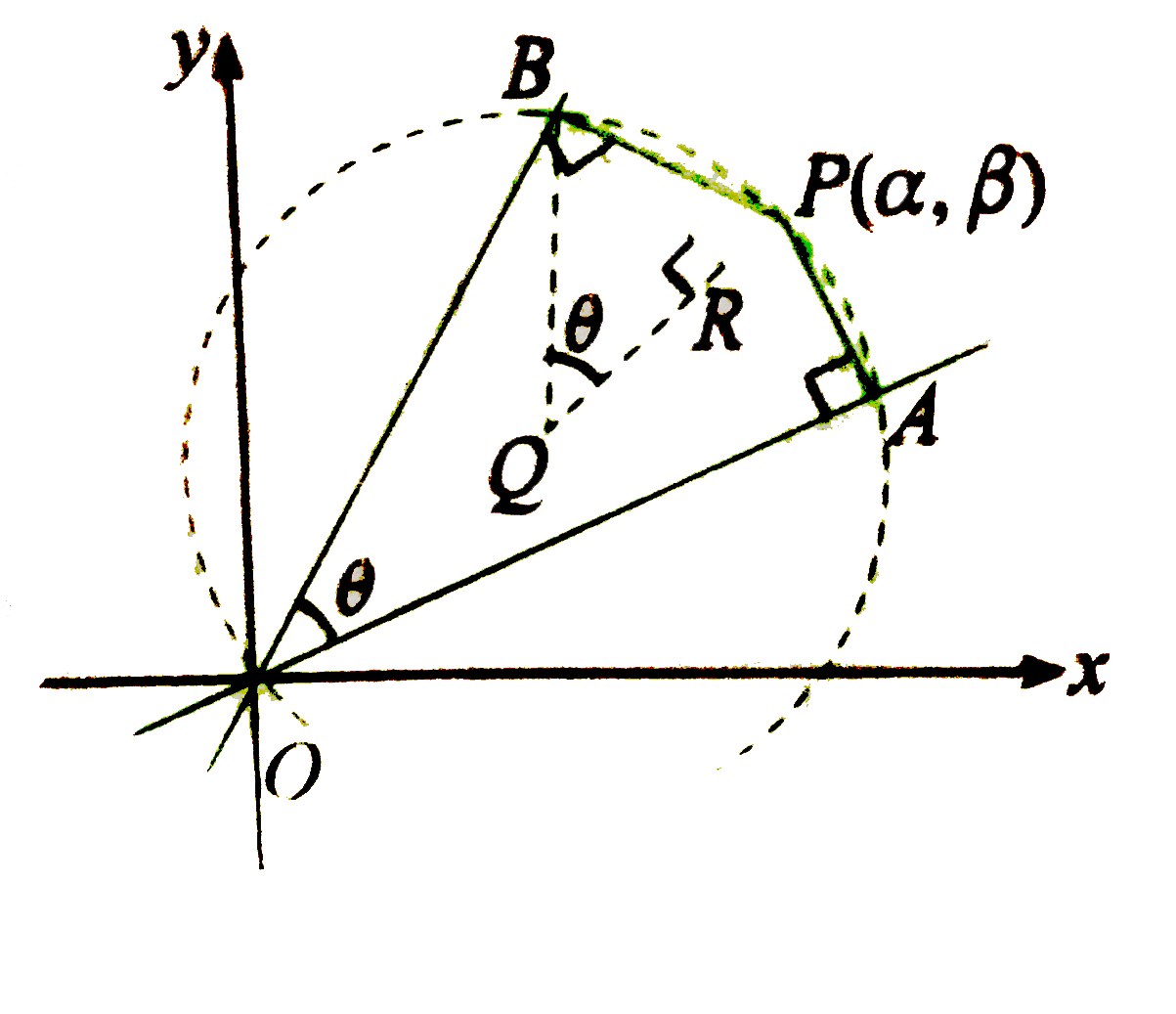
From point perpendiculars are dropped on the given pair of lines.
According to the question , AB=2d. Clearly OAPB is a cyclic quadrilateral and OP will be the diameter of the circumcircle of this quadrilateral.
Let Q be the center of the circle.
therefore , in ,
(1)
Also , angle between the lines is
(2)
Therefore , from (1) and (2), we get
Therefore , the locus of is
Topper's Solved these Questions
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise 3.1
6 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise 3.2
7 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Illustration 3.17
1 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Matching Column Type
1 Videos
Similar Questions
Find the combined equation of the pair of lines through the point (1, 0) and parallel to the lines represented by 2x2−xy−y2=0
View SolutionIf the slope of one line is double the slope of another line and the combined equation of the pair of lines is (x2a)+(2xyh)+(y2b)=0 , then find the ratio ab:h2.
View SolutionProve that the angle between the lines joining the origin to the points of intersection of the straight line y=3x+2 with the curve x2+2xy+3y2+4x+8y−11=0 is tan−1(2√23)
View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?
View SolutionAB is a chord of y2=4x such that normals at A and B intersect at C(9,6) and the tengent at A and B at point T, find (CT)2/13
View SolutionA point moves so that the distance between the foot of perpendiculars from it on the lines ax2+2hxy+by2=0 is a constant 2d . Show that the equation to its locus is (x2+y2)(h2−ab)=d2{(a−b)2+4h2}.
View SolutionThe locus of the foot of the perpendicular from the foci an any tangent to the ellipse x2a2+y2b2=1, is
View SolutionThe locus of the point of intersection of the perpendicular tangents to the circle x2+y2=a2,x2+y2=b is
View SolutionThe locus of foot of perpendicular from focus of ellipse x2a2+y2b2=1 to its tangents is
View SolutionHyperbola x^2/a^2-y^2/b^2=1 Is the locus of the foot of the perpendicular inserted from the center of
View SolutionProve that the product of the perpendiculars from (α,β) to the pair of lines ax2+2hxy+by2=0 is aα2+2hαβ+bβ2√(a−b)2+4h2
View SolutionA point moves so that the distance between the foot of perpendiculars from it on the lines ax2+2hxy+by2=0 is a constant 2d . Show that the equation to its locus is (x2+y2)(h2−ab)=d2{(a−b)2+4h2}.
View SolutionProve that the product of the perpendiculars from (α,β) to the pair of lines ax2+2hxy+by2=0 is aα2+2hαβ+bβ2√(a−b)2+4h2
View SolutionA plane passes through a fixed point (a,b,c). Show that the locus of the foot of the perpendicular to it from the origin is the sphere x2+y2+z2−ax−by−cz=0.
View SolutionA plane passes through a fixed point (a,b,c). Show that the locus of the foot of the perpendicular to it from the origin is the sphere x2+y2+z2−ax−by−cz=0.
View SolutionA point moves so that the sum of its distances from (ae,0)and(−ae,0) is 2a, prove that the equation to its locus is x2a2+y2b2=1 , where b2=a2(1−e2).
View Solution
