A point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.Solution in Bengali
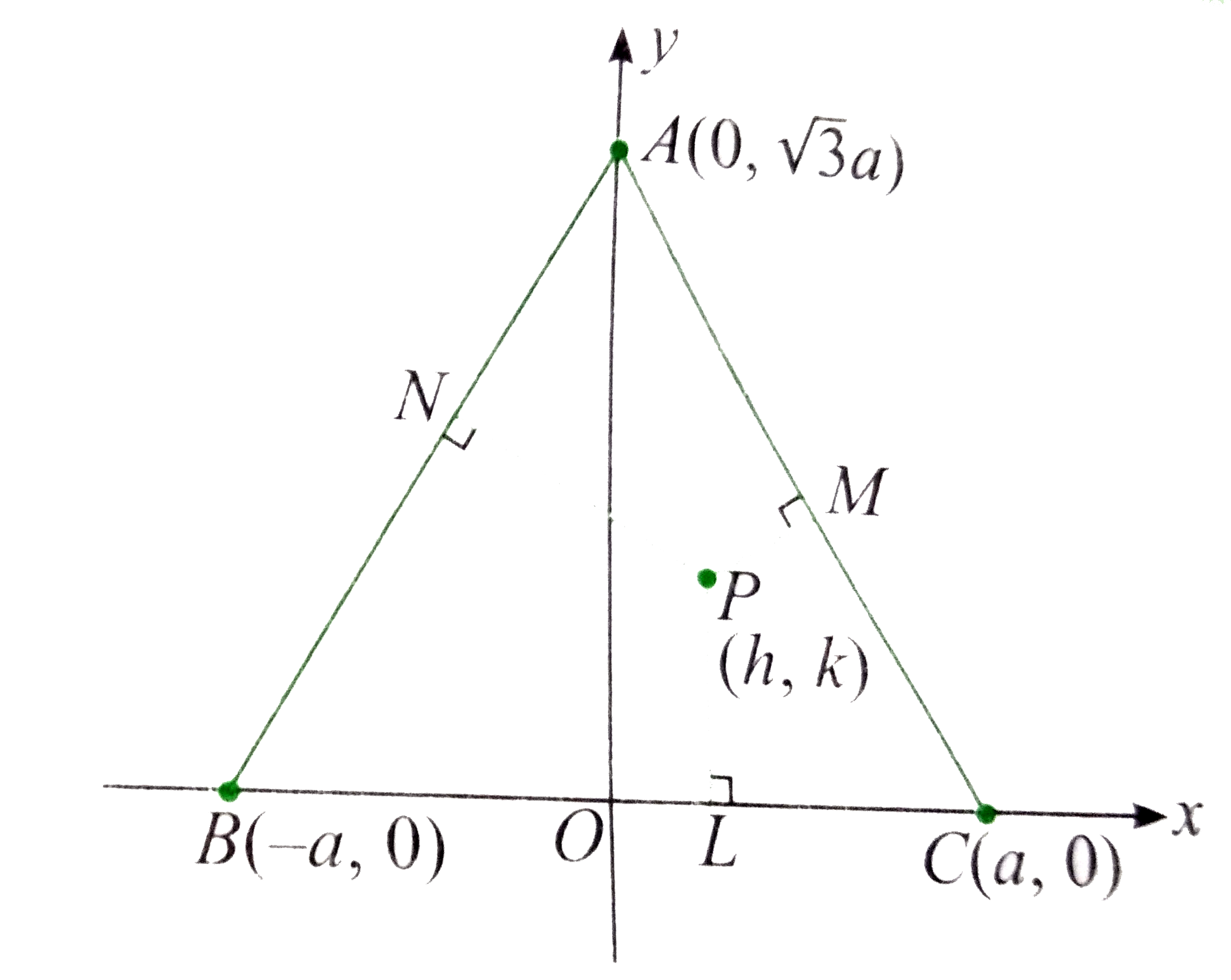
Let vertices B and C of equilateral triangle be (-a,0) and (a,0)
OA=OBtan60∘=a√3
∴A≡(0,a√3)
Let point P be (h,k).
Equations of AC and BC are x√3+y−a√3=0 and x√3−y+a√3=0, respectively.
According to the question,
PL2+PM2+PN2= constant (say λ)
∴k2+(√3h+k−√3a2)2+(√3h−k+√3a2)2=λ
⇒6h2+6k2−4√3ak+6a2−4λ=0
Hence, the required locus is 6x2+6y2−4√3ay+6a2−4λ=0 which is a circle
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Examples
13 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The line Ax+By+C=0 cuts the circle x2+y2+ax+by+c=0 at PandQ . The line A′x+B′x+C′=0 cuts the circle x2+y2+a′x+b′y+c′=0 at RandS. If P,Q,R, and S are concyclic, then show that |a−a'b−b'c−c'ABCA'B'C'|=0
View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View SolutionProve that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
View SolutionA point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.
View SolutionFind the locus a point which moves in such a way that the sum of squares of its distances s from the four sides of a square is constant. Does it represent a circle?
View SolutionThe locus of a point which moves such that the sum of the squares of the distances from the three vertices of a triangle is constant, is a circle whose centre is at the:
View SolutionIf a point moves so that sum of the square of the perpendiculars from it on the side of an equilateral triangle is consant then its locus is a
View SolutionProve that the sum of the perpendiculars drawn from any interior point of an equilateral triangle to its sides then sum of three perpendiculars is equal to the altitude of the triangle.
View SolutionA point moves so that sum of the squares of its distances from the vertices of a triangle is always constant. Prove that the locus of the moving point is a circle whose centre is the centroid of the given triangle.
View SolutionProve that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
View SolutionA point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.
View SolutionA point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View Solution
