A point P moves inside a triangle formed by A(0,0),B(1,√3),C(2,0) such that min {PA,PB,PC)=1, then the area bounded by the curve traced by P, is Solution in Punjabi
(a)3√3−3π2
(b)√3+π2
(c)√3−π2
(d)3√3+3π2
The correct Answer is:C
Step by step video & image solution for A point P moves inside a triangle formed by A(0,0),B(1,sqrt(3)),C(2,0) such that min {PA,PB,PC)=1, then the area bounded by the curve traced by P, is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Single Option Correct Type Questions)24videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (More Than One Correct Option Type Questions)5videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise For Session 110videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)21videos
BIONOMIAL THEOREM
Similar Questions
A point P(x,y) moves such that [x+y+1]=[x]. Where [.] denotes greatest intetger function and x∈(0,2), then the area represented by all the possible position of P , is
02:47View SolutionThe triangle formed by the normal to the curve f(x)=x2−ax+2a at the point (2,4) and the coordinate axes lies in second quadrant, if its area is 2 sq units, then a can be
03:48View SolutionDraw a rough sketch of y=sin2x and determine the area enclosed by the curve. X-axis and the lines x=π/4 and x=3π/4.
03:00View SolutionThe value of (300)(3010)−(301)(3011)+(302)(3012)+....+(3020)(3030)
02:28View SolutionA point P moves inside a triangle formed by A(0,0),B(1,sqrt(3)),C(2,0) such that min{PA,PB,PC}=1, then the area bounded by the curves traced by P is:
View SolutionIf AB,AC,AD, and AE are parallel to a line l, then points A,B,C,D and E are collinear
10:00View SolutionTwo lines which are parallel to the same line, are parallel to each other
07:11View SolutionIf P is a point inside Delta ABC such that BC(vec PA)+CA(vec PB)+AB(vec PC)=vec O then P is the .....
01:56View SolutionLet A(12,0),B(32,0),C(52,0) be the given points and P be point sashaying max (PA+PB,PB+PC)<2. If area of region of point P is √3(πa−√3b) then a+b is
03:17View SolutionP is a point inside the equilateral traingle ABC such that PA=1cm,PB=√2cm and PC=√3. Then the side of the traingle (in cm) equal.
02:24View SolutionLet ABC be a triangle and P be a point inside ABC such that −−→PA+2−−→PB+3−−→PC=→0. The ratio of the area of triangle ABC to that of APC is - (A) 2 (B) 32(C) 53 (D) 3
View SolutionIn a cricle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
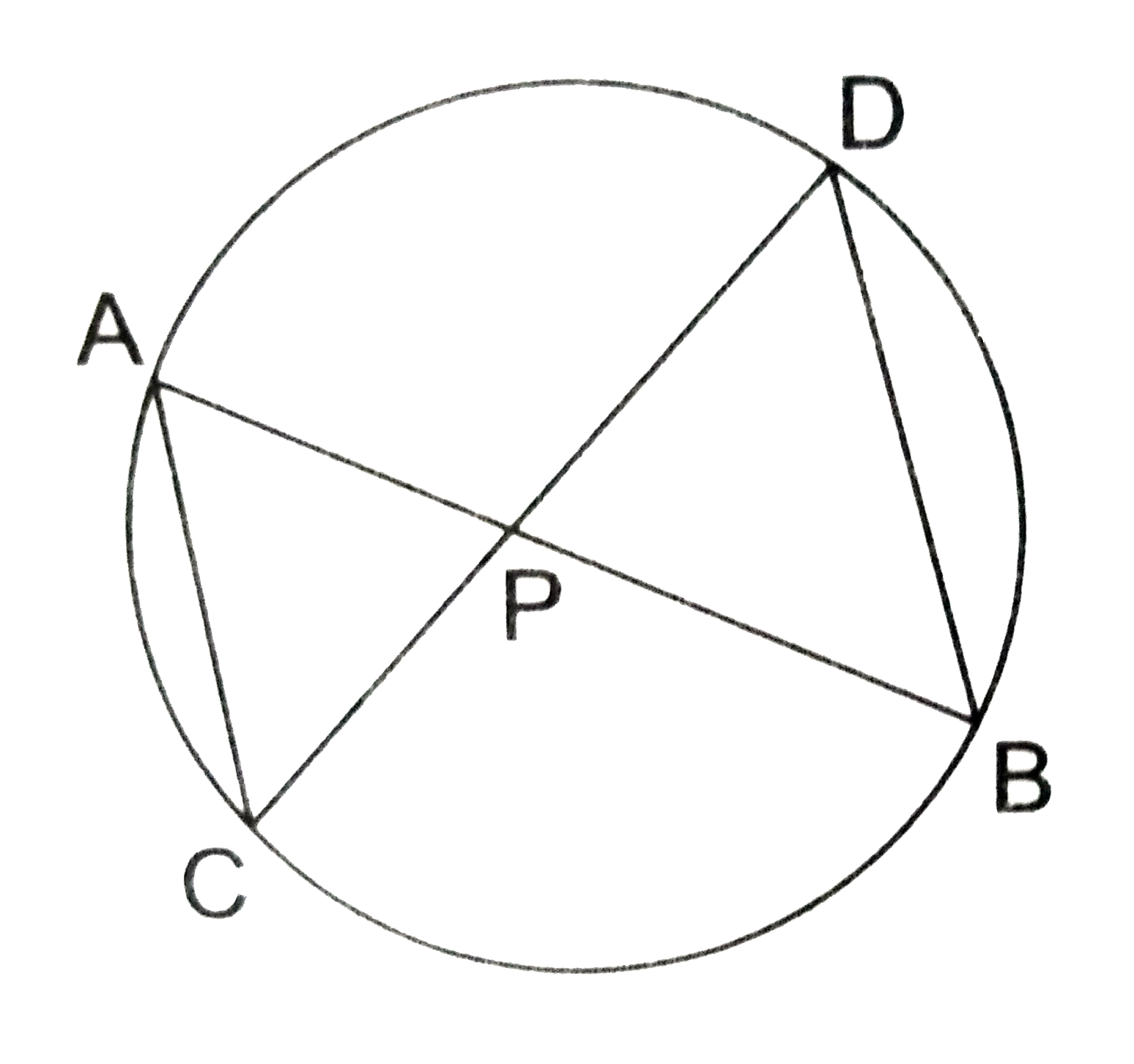 04:53View Solution
04:53View SolutionABC is an equilateral triangle where AB = a and P is any point in its plane such that PA = PB + PC. Then PA2+PB2+PC2a2 is
04:35View SolutionIf P is a point on the plane of ΔABC such that ¯¯¯¯¯¯PA+¯¯¯¯¯¯PB+¯¯¯¯¯¯PC=0, then, for Δ ABC, the point P is
06:07View SolutionA point P moves inside a triangle formed by A(0,0),B(1,1√3),C(2,0) such that min {PA,PB,PC)=1, then the area bounded by the curve traced by P, is
05:09View SolutionA point P moves inside a triangle formed by A(0,0),B(2,2√3),C(4,0) such that {min (PA, PB, PC)} = 2, then the area bounded by the curve traced by P is
05:31View Solution

