A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
To solve the problem, we need to determine if it is possible to erect a pole on the boundary of a circular park such that the difference in distances from two diametrically opposite gates A and B is 7 meters. The diameter of the park is given as 13 meters.
1. Identify the Given Information:
- Diameter of the circular park = 13 meters.
- The difference in distances from the pole to gates A and B = 7 meters.
2. Calculate the Radius:
- Radius r=Diameter2=132=6.5 meters.
3. Set Up the Problem:
- Let the distance from the pole to gate A be PA=x.
- Therefore, the distance from the pole to gate B will be PB=x+7 (since PB−PA=7).
4. Use the Relationship of Distances:
- The distance between gates A and B (the diameter) is 13 meters. According to the Pythagorean theorem:
AB2=PA2+PB2
- Here, AB=13 meters, so:
132=x2+(x+7)2
5. Expand and Simplify the Equation:
- Expanding (x+7)2:
169=x2+(x2+14x+49)
- Combine like terms:
169=2x2+14x+49
- Rearranging gives:
2x2+14x+49−169=0
2x2+14x−120=0
6. Divide the Equation by 2:
- Simplifying the equation:
x2+7x−60=0
7. Factor the Quadratic Equation:
- We need to find two numbers that multiply to −60 and add to 7. The numbers are 12 and −5:
(x+12)(x−5)=0
8. Solve for x:
- Setting each factor to zero gives:
x+12=0⇒x=−12(not possible, as distance cannot be negative)
x−5=0⇒x=5
9. Determine the Distances:
- Distance from gate A (PA) = x=5 meters.
- Distance from gate B (PB) = x+7=5+7=12 meters.
10. Conclusion:
- Yes, it is possible to erect the pole. The distances from the two gates should be:
- Distance from gate A = 5 meters
- Distance from gate B = 12 meters
- Diameter of the circular park = 13 meters.
- The difference in distances from the pole to gates A and B = 7 meters.
- Radius r=Diameter2=132=6.5 meters.
- Let the distance from the pole to gate A be PA=x.
- Therefore, the distance from the pole to gate B will be PB=x+7 (since PB−PA=7).
- The distance between gates A and B (the diameter) is 13 meters. According to the Pythagorean theorem:
AB2=PA2+PB2
- Here, AB=13 meters, so:
132=x2+(x+7)2
- Expanding (x+7)2:
169=x2+(x2+14x+49)
- Combine like terms:
169=2x2+14x+49
- Rearranging gives:
2x2+14x+49−169=0
2x2+14x−120=0
- Simplifying the equation:
x2+7x−60=0
- We need to find two numbers that multiply to −60 and add to 7. The numbers are 12 and −5:
(x+12)(x−5)=0
- Setting each factor to zero gives:
x+12=0⇒x=−12(not possible, as distance cannot be negative)
x−5=0⇒x=5
- Distance from gate A (PA) = x=5 meters.
- Distance from gate B (PB) = x+7=5+7=12 meters.
- Yes, it is possible to erect the pole. The distances from the two gates should be:
- Distance from gate A = 5 meters
- Distance from gate B = 12 meters
Similar Questions
A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected?
View Solution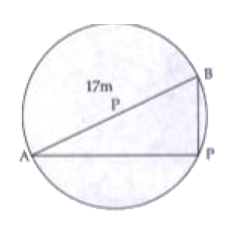
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
What is the length of (AP+BP) ?View Solution
Knowledge Check
- Question 1 - Select One
The locus of a point which moves so that the difference of the squares of its distances from two given points is constant, is a
Astraight lineBplaneCsphereDnone of these - Question 2 - Select One
The locus of a point which moves so that the difference of the squares of its distance from two given points is constant, is a
Astraight lineBplaneCsphereDNone of these - Question 3 - Select One
A vertical pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point β on the boundary. If the chord AB subtends an angle α at the centre of the park, the height of the pole is
A2a sinα2tanαB2a cosα2tanαC2a sinα2cotαD2a cosα2cotα

Aniket is studying in X standard. He created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the area of triangle ABP.View Solution
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the distance between pole and gate B.View Solution
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the distance between pole and gate A.View Solution
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find a quadratic equations in variable x for above situation.View SolutionA point P moves in such a way that the ratio of its distance from two coplanar points is always a fixed number (≠1) . Then, identify the locus of the point.
View Solution

