A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible t
Step by step video & image solution for A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible t by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 03 (MATHEMATICS)EXERCISE - SECTION C15videos
SAMPLE PAPER 03 (MATHEMATICS)
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 03EXERCISE - Section - C10videos
SAMPLE PAPER 03
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 07EXERCISE - SECTION -C10videos
SAMPLE PAPER 07
Similar Questions
A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected?
View Solution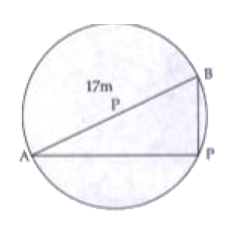
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the distance between pole and gate B.View Solution
Knowledge Check
- Question 1 - Select One
A point P is moving in a plane such that the difference of its distances from two fixed points in the same plane is a constant. The path traced by the point P is a/an
ACircleBparabolaCEllipseDHyperbola - Question 2 - Select One
A pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point B on the boundary. If the chord AB subtends an angle α at the centre of the path, the height of the pole is
A2acos(α/2)tanαB2asin(α/2)cotαC2asin(α/2)tanαD2acos(α/2)cotα

Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the distance between pole and gate A.View Solution
Aniket is studying in X standard. He created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the area of triangle ABP.View Solution
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find a quadratic equations in variable x for above situation.View Solution
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
What is the length of (AP+BP) ?View SolutionA point P moves in such a way that the ratio of its distance from two coplanar points is always a fixed number (≠1) . Then, identify the locus of the point.
View SolutionTo find the equation of the hyperbola from the definition that hyperbola is the locus of a point which moves such that the difference of its distances from two fixed points is constant with the fixed point as foci
View Solution

