A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC
Step by step video & image solution for A quadrilateral ABCD is drawn to circumscribe a circle. Prove that A B+C D=A D+B C by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MATHEMATICS BASICBOOK - CBSE MODEL PAPERCHAPTER - MATHEMATICS BASICEXERCISE - PART A (SECTION -II)
20 Videos
- Additional Practice QuestionsBOOK - CBSE MODEL PAPERCHAPTER - Additional Practice QuestionsEXERCISE - Question
44 Videos
- SAMPLE PAPER (MATHEMATICS STANDARD)BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER (MATHEMATICS STANDARD)EXERCISE - PART - A
15 Videos
Similar Questions
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC
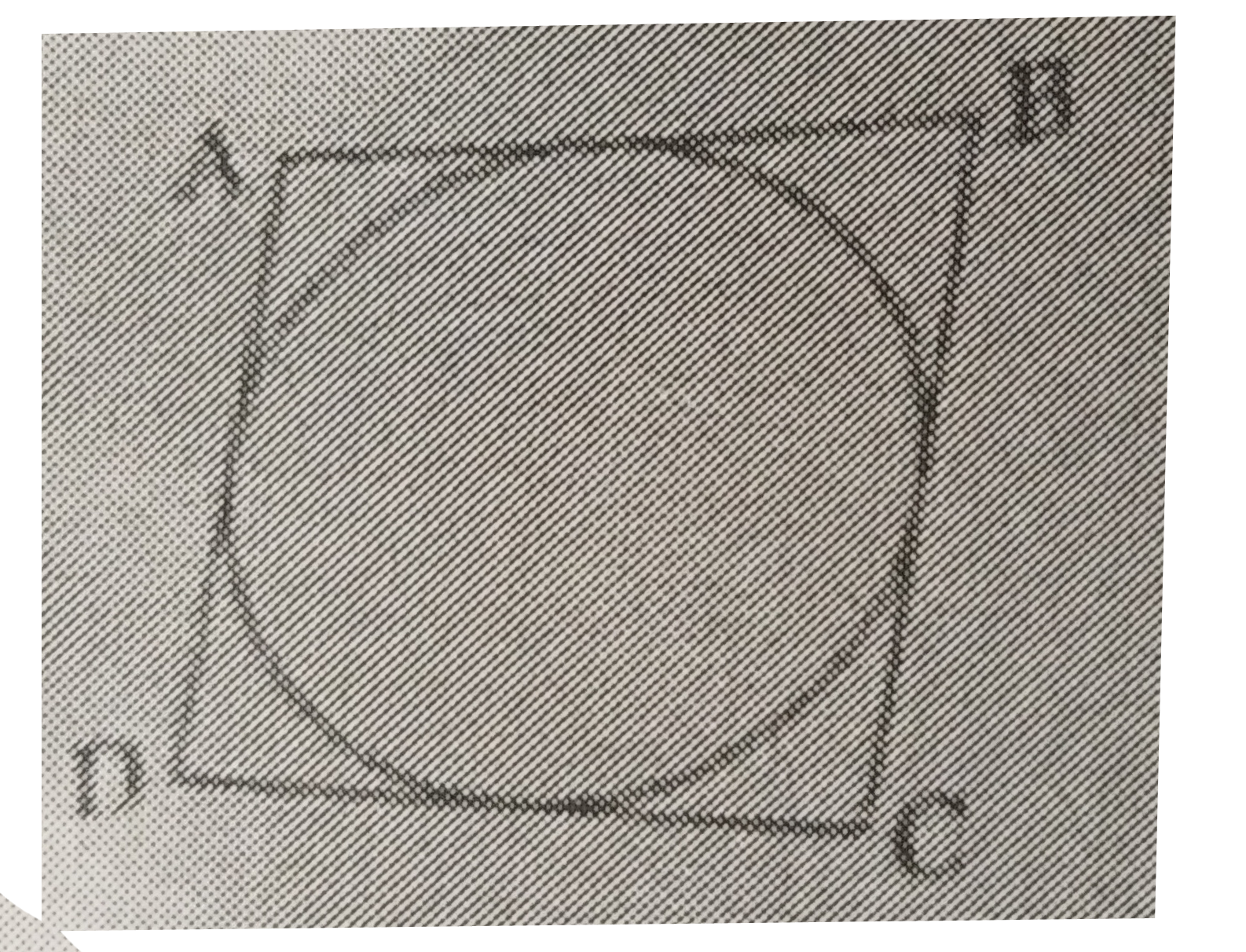
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC.
or
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB+CD=BC+DA.
View SolutionIn Fig. 10.103, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB=x cm , BC=7cm , CR=3cm and AS=5cm , then x= (FIGURE) (a) 10 (b) 9 (c) 8 (d) 7
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
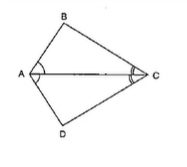
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionProve that the diagonals of quadrilateral ABCD,AC and BD intersect in O. Prove that if BO=OD, the triangles ABC and ADC are equal in area.
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View Solution