A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of the rectangle so that its area is maximum. Find also the area.
The correct Answer is:length =r√2, breadth =r√22, area =r2 sq units
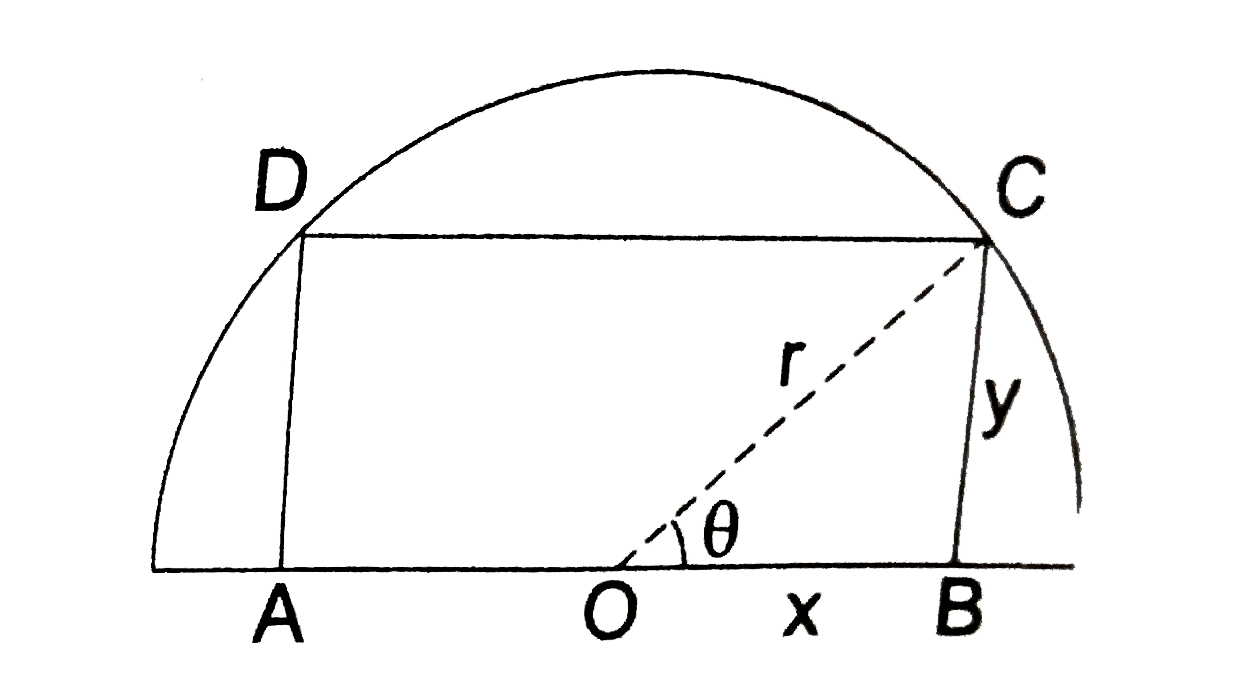
Let ABCD be the rectangle of length 2x and breadth y, inscribed in a semicircle of radius r and centre O. Let ∠BOC=θ
Then, yr=sinθandxr=cosθ
∴ area of the rectangle is given by
A=2xy=r2sin2θ
⇒dAdθ=2r2cos2θandd2Adθ2=−4r2sin2θ
Now, dAdθ=0⇒cos2θ=0⇒2θ=π2⇒θ=π4
For this value of θ, we have d2Adθ2=−4r2<0
∴ area is maximum when 2x=2rcosπ4=r√2andy=rsin π4=r√22
Maximum area =2xy=r√2×r√22=r2 sq units.
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11G
Explore 32 Videos
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11H
Explore 30 Videos
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11E
Explore 22 Videos
- ADJOINT AND INVERSE OF A MATRIXBook:RS AGGARWALChapter:ADJOINT AND INVERSE OF A MATRIXExercise:Exercise 7
Explore 37 Videos
- AREA OF BOUNDED REGIONS Book:RS AGGARWALChapter:AREA OF BOUNDED REGIONS Exercise:Exercise 17
Explore 39 Videos
Similar Questions
A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of rectangle so that the area is maximum. Find the area also.
View SolutionThe perimeter of a rectangle is 40 cm. Find the dimensions of the rectangle if its area is maximum.
View Solution
Knowledge Check
A rectangle is inscribed in a semicircle of radius 1 unit. If its two vertices lie on the diameter, for largest size, then its dimensions are
ALength =√2, breadth =1√2BLength =√3, breadth =12CLength =2√3√2, breadth =13DLength =1√2, breadth =√2The maximum area of rectangle, inscribed in a circle of radius 'r', is :
Aπr2Br2C2r2D14πr2The largest triangle is inscribed in a semi-circle of radius 4 cm. Find the area inside the semi-circle which is not occupied by the triangle.
A8(π−2)sqcmB7(π−1)sqcmC6(π−2)sqcmDNone of these
A wire of length 16 cm is bent to form a rectangle. Find the dimensions of the rectangle so that it has the maximum area
View SolutionRectangles are inscribed inside a semi-circle of radius r. Find the rectangle with maximum area.
View SolutionShow that the rectangle of maximum area that can be inscribed in a circle is a square.
View SolutionRectangles are inscribed inside a semicircle of radius r. Find the rectangle with maximum area.
View SolutionA rectangle of sides a and b is inscribed in a circle. Then its radius is
View Solution
