Question

A rectangle with sides of lengths $(2n-1)\text{and}(2m-1)$ units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is

Options

A. `m^(2)n^(2)`
B. `mn(m+1)(n+1)`
C. `4^(m+n-1)`
D. none of these

Answer

A

Explanation

Clearly,
Number of horizontal rectangles of 1 units length `=(2m-1)`
Number of horizontal rectangles of 3 unit length `=(2m-3)`
Number of horizontal rectangles of 5 unit length `=(2m-5)`
Similarly,
Number of rectangles of `(2m-1)` unit length =1
`:.` Total number of horizontal rectangles of odd length
`=(2m-1)+(2m-3)+....+3+1=m^(2)`

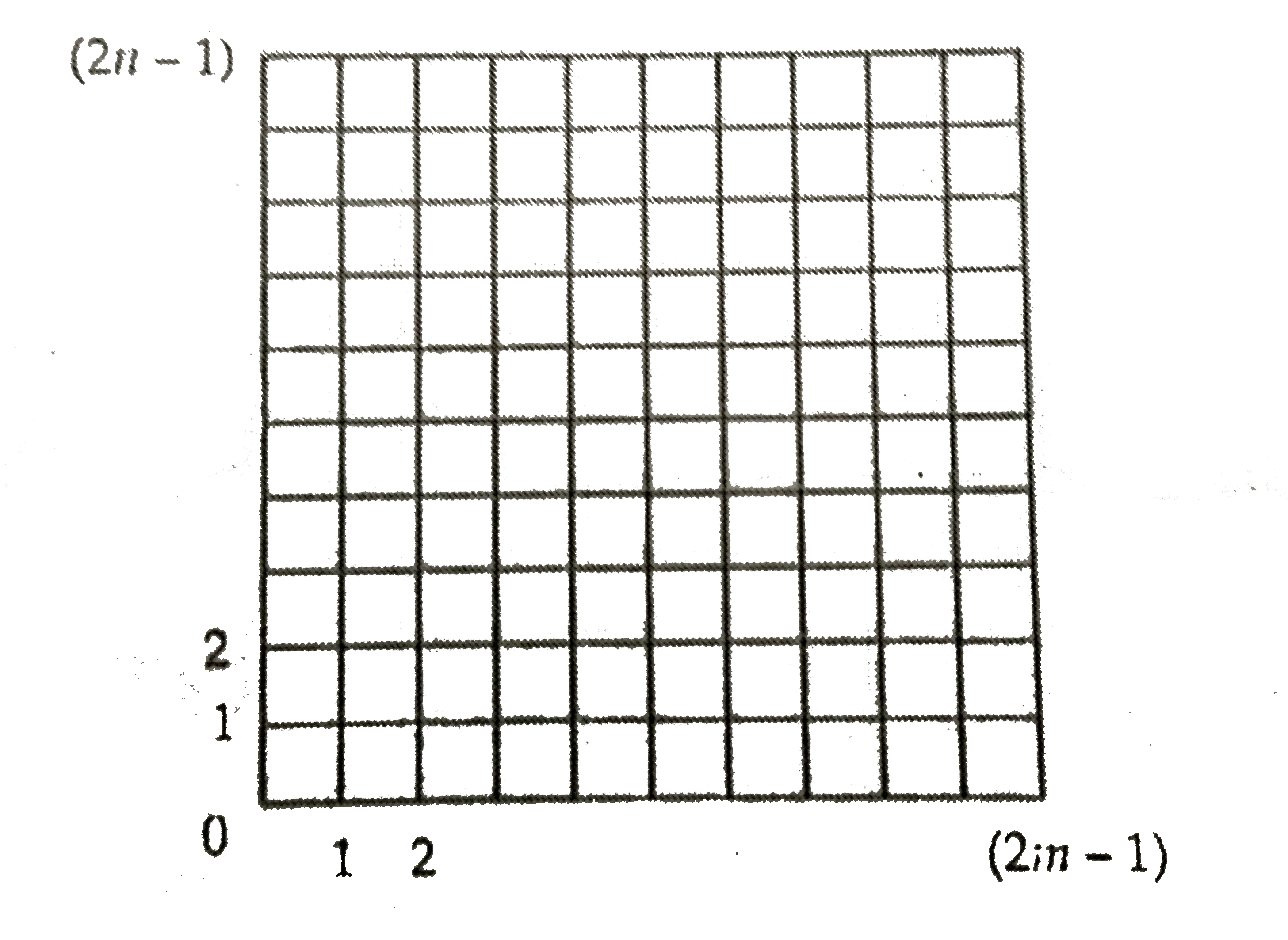
Similarly
Total number vertical rectangles of odd length `=n^(2)`
`:.` Total numbr of rectangles `=m^(2)xxn^(2)`