A rectangular billiard table has vertices at P(0,0),Q(0,7),R(10,7), and S(10,0). A small billiard ball starts at M(3,4) , moves in a straight line to the top of the table, bounces to the right side of the table, and then comes to rest at N(7,1) . The y− coordinate of the point where it hits the right side is 3.7 (b) 3.8 (c) 3.9 (d) 4
3.7
3.8
3.9
4
The correct Answer is:A
tanθ=a−13=7−a10−b
Also, tanθ=7−4b−3=3b−3
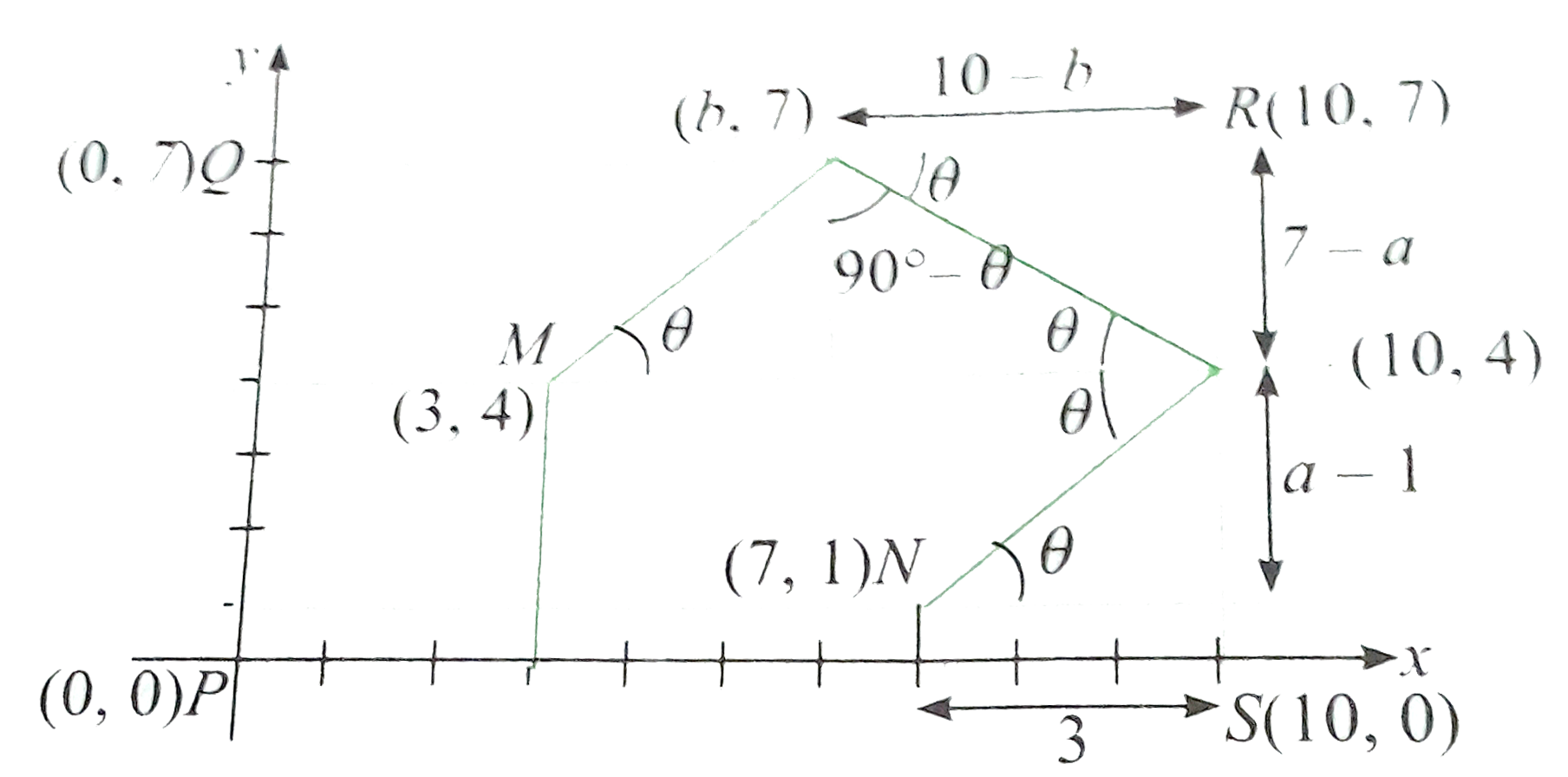
Hence, 3b−3=a−13=7−a10−b
From the first two relations, we have
9=ab−b−3a+3
or 3a+6=ab−b
From the last two relations, we have
10a−ab−10+b=21−3a
or 3a−ab+b=31
or ab−b=13a−31
Hence, from (1) and (2) ,
3a+6=13a−31
or 10a−37
or a=3.7
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct13videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Linked10videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.69videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
A rectangular billiard table has vertices at P(0,0),Q(0,7),R(10,7), and S(10,0). A small billiard ball starts at M(3,4) , moves in a straight line to the top of the table, bounces to the right side of the table, and then comes to rest at N(7,1) . The y− coordinate of the point where it hits the right side is (a)3.7 (b) 3.8 (c)3.9(d) 4
View SolutionFind the co-ordinates of the point of intersection of the straight lines
2x−3y−7=0,3x−4y−13=0View Solution
Knowledge Check
- Question 1 - Select One
A point R with x - coordinate 4 lies on the line segment joining the points P(2,-3,4) and Q(8, 0, 10) . The coordinates of R are
A(4, -2, 6)B(-4,-2,6)C(-4,2,6)D(4,2,6)
Write the coordinates of the image of the point (3,8) in the lines x+3y−7=0.
View SolutionA point R with x-coordinates 4 lies on the line segment joining the points P(2,−3,4)and Q(8,0,10). Find the coordinates of the point R.
View SolutionA man starts from the point P(−3,4) and will reach the point Q(0,1) touching the line 2x+y=7 at R. The coordinates R on the line so that he will travel in the shortest distance is
View SolutionOne side of a rectangle lies along the line 4x+7y+5=0. Two of its vertices are (−3,1)and(1,1). Find the equations of the other three sides.
View SolutionOne side of a rectangle lies along the line 4x+7y+5=0. Two of its vertices are (−3,1)and(1,1). Find the equations of the other three sides.
View SolutionOne side of a rectangle lies along the line 4x+7y+5=0. Two of its vertices are (−3,1) and (1,1). Find the equations of the other three sides.
View SolutionIf the coordinates of the mid-points of the sides of a triangle are (3,4),(4,6)and(5,7), find its vertices.
View Solution

