A rectangular piece is 20m and 15m wide. From its four corners, quadrants of radii 3.5m have been cut. Find the area of the remaining part.
To find the area of the remaining part of the rectangular piece after cutting out the quadrants from its corners, we can follow these steps:
Step 1: Calculate the area of the rectangle
The area of a rectangle is given by the formula:
Area of rectangle=Length×Width
Given the length is 20 m and the width is 15 m, we can calculate:
Area of rectangle=20m×15m=300m2
Step 2: Calculate the area of one quadrant
The area of a quadrant (which is a quarter of a circle) can be calculated using the formula for the area of a circle:
Area of circle=πr2
Since we need the area of one quadrant, we will divide the area of the full circle by 4. Given the radius r=3.5m:
Area of circle=π(3.5)2=π×12.25≈38.5m2
Now, the area of one quadrant is:
Area of one quadrant=38.54≈9.625m2
Step 3: Calculate the total area of the four quadrants
Since there are four quadrants cut from the corners of the rectangle, we multiply the area of one quadrant by 4:
Total area of four quadrants=4×9.625≈38.5m2
Step 4: Calculate the area of the remaining part
To find the area of the remaining part, we subtract the total area of the quadrants from the area of the rectangle:
Area of remaining part=Area of rectangle−Total area of quadrants
Area of remaining part=300m2−38.5m2=261.5m2
Final Answer
The area of the remaining part is:
Area of remaining part=261.5m2
---
The area of a rectangle is given by the formula:
Area of rectangle=Length×Width
Given the length is 20 m and the width is 15 m, we can calculate:
Area of rectangle=20m×15m=300m2
The area of a quadrant (which is a quarter of a circle) can be calculated using the formula for the area of a circle:
Area of circle=πr2
Since we need the area of one quadrant, we will divide the area of the full circle by 4. Given the radius r=3.5m:
Area of circle=π(3.5)2=π×12.25≈38.5m2
Now, the area of one quadrant is:
Area of one quadrant=38.54≈9.625m2
Since there are four quadrants cut from the corners of the rectangle, we multiply the area of one quadrant by 4:
Total area of four quadrants=4×9.625≈38.5m2
To find the area of the remaining part, we subtract the total area of the quadrants from the area of the rectangle:
Area of remaining part=Area of rectangle−Total area of quadrants
Area of remaining part=300m2−38.5m2=261.5m2
The area of the remaining part is:
Area of remaining part=261.5m2
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - LINEAR EQUATION IN ONE VARIABLEEXERCISE - All Questions107videos
LINEAR EQUATION IN ONE VARIABLE
- BOOK - RD SHARMACHAPTER - MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)EXERCISE - All Questions134videos
MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)
Similar Questions
Knowledge Check
- Question 1 - Select One
A square park has each side 50 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 7 m, as shown in the figure. Find the area of remaining part of the park.
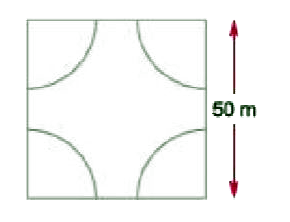 A2346 sq mB2340 sq mC2250 sq mD2155 sq m
A2346 sq mB2340 sq mC2250 sq mD2155 sq m - Question 2 - Select One
The floor of a rectangular room is 15 m long and 12 m wide. The room is surrounded by a verandah of width 2 m on all its sides. The area of the verandah is:
A124m2B120m2C108m2D58m2
A rectangular sheet of acrylic is 34 cm by 24 cm. From it, 64 circular buttons, each ofdiameter 3.5 cm, have been cut out. Find the area of the remaining sheet.
View SolutionA rectangular park is 2034 m long and 1512 m wide. What is the area of the park?
View SolutionA square park has each side of 100 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in Fig. 15.37. Find the area of the remaining part of the park (Use π=22/7) . (FIGURE)
View SolutionEach side of a square park is 80 m. At each corner of the park there is a flower bed in the form of a quadrant of a circle of radius 14 m, as shown in the figure. Find the area of the remaining part of the park.
View SolutionFrom a ribbon of length 15m, two pieces of 7m and 6.5m were cut. Find the length of remaining piece.
View SolutionIn each of the corners, there is a flower bed in the form of a quadrant of a circle of radius 2 m. Also, there is a flower bed in the form of a circle of radius 2 m in the middle of the plot. Find the area of the remaining plot.
 View Solution
View Solution

