A regular square based pyramid is inscribed in a sphere of given radius R so that all vertices of the pyramid belong to the sphere. Find the greatest value of the volume of the pyramid.
The correct Answer is:6481r3
If we cut the sphere from the center along the diagonal of the square base we get the view show in figure

Let r be the radius of the spere Then
Height of the pyramid =r+r cosθ
Diagonal of the square base =2rsinθ
∴ side of the squre base =2rsinθ√2
Let v be the volume of the pyaramid .Then
V=13 (Area of the base xx Height)
=132rsinθ(√2)2×(r+rcosθ)
∴dVdθ=23r3[sin2θ(1+cosθ)−sin3θ]
=23r3[2sin2θcos2θ−sin3θ]
=23r3×sinθ(2cosθ+2cos2θ−sin2θ)
=23r3sinθ(3cos2θ+2cosθ−1)
=23r3sinθ(cosθ+1)(3cosθ−1)
For maximum or minimum values of v we must have dVdθ=0
or 3cosθ−1=0
cos θ=13
Hence V is maximum when cos θ=13andsinθ=2√23
The maximum value of V is given by
V=23r3×89(1+13)=6481r3
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise
92 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Multiple correct answers type
48 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.6
9 Videos
- METHODS OF DIFFERENTIATIONBOOK - CENGAGE PUBLICATIONCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Multiple Correct Answer Type
7 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
The lateral edge of a regular rectangular pyramid is acmlong. The lateral edge makes an angle α with the plane of the base. Find the value of α for which the volume of the pyramid is greatest.
View SolutionThe lateral edge of a regular rectangular pyramid is acmlong. The lateral edge makes an angle α with the plane of the base. Find the value of α for which the volume of the pyramid is greatest.
View Solution
Knowledge Check
Height of greatest cone inscribed in a sphere of radius r is
A2r3Br3C3r2D4r3A cylinder is inscribed in a sphere of radius r
What is the radius of the cylinder of maximum volume ?A2r√3B√2√3rCrD√3rA prism and a pyramid have the same base and the same height. Find the ratio of the volumes of the prism and the pyramid.
A1:1B1:3C3:1DCannot be determined
Height of a cone, inscribed in a sphere of radius r, having greatest curved surface is
View SolutionThe base of a pyramid is a square whose side is 10 cm. It's slant and vertical heights are 13 and 12 . Then , find the total surface area and volume of the pyramid .
View SolutionProve that the volume of the largest cone that can be inscribed in a sphere of radius R is 827of the volume of the sphere.
View SolutionA regular square pyramid is placed in a cube so that the base of the pyramid and that of the cube coincide. The vertex of the pyramid lies on the face of the cube opposite to the base, as shown. An edge of the cube is 7 inches.
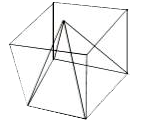
How many square inches (approximately) are in the posi- tive difference between the surface area of the cube and the surface area of the pyramid ?
View SolutionA regular pyramid has a square base. The height of the pyramid is 22 cm and side of its base is 14 cm. Volume of pyramid is equal to the volume of a sphere. What is the radius (in cm) of the sphere?
View Solution
