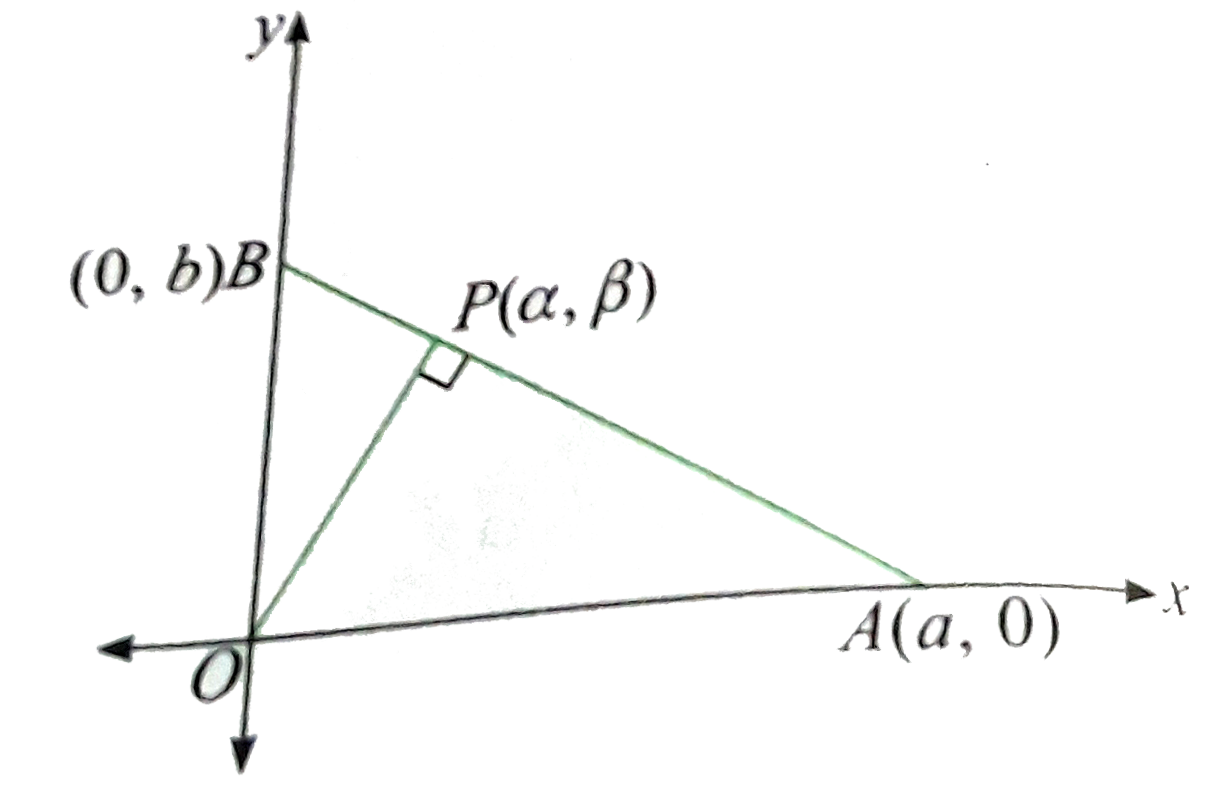
A rod of length k slides in a vertical plane, its ends touching the coordinate axes. Prove that the locus of the foot of the perpendicular from the origin to the rod is (x2+y2)3=k2x2y2.
(Slope of OP). (Slope of BP)=−1
or βα.β−bα−0.=−1
or b=α2+β2β
and (Slope of OP).(Slope of AP)=−1
or βα.βα−α.=−1
∴a=α2+β2α
Now, a2+b2=k2
∴(a2_β2)3=k2a2β2
∴(x2+y2)3=k2x2y2
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.2
8 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.67
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
The locus of the foot of the perpendicular from the centre of the ellipse x2+3y2=3 on any tangent to it is
View SolutionFind the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0.
View SolutionThe locus of the foot of the perpendicular from the foci an any tangent to the ellipse x2a2+y2b2=1, is
View Solutionthe locus of the foot of perpendicular drawn from the centre of the ellipse x2+3y2=6 on any point:
View SolutionFind the coordinates of the foot of perpendicular drawn from origin to the planes: x+y+z=1
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point (2,3) to the line y=3x+4
View SolutionA plane passes through a fixed point (a,b,c). Show that the locus of the foot of the perpendicular to it from the origin is the sphere x2+y2+z2−ax−by−cz=0.
View SolutionA plane passes through a fixed point (a,b,c). Show that the locus of the foot of the perpendicular to it from the origin is the sphere x2+y2+z2−ax−by−cz=0.
View SolutionFind the coordinates of the foot of perpendicular drawn from origin to the planes: 2x+3y+4z−12=0
View Solution
