A solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy.
To find the volume of the wooden toy that is in the shape of a right circular cone mounted on a hemisphere, we can follow these steps:
Step 1: Identify the dimensions
- The radius of the hemisphere (and cone) is given as r=4.2 cm.
- The total height of the toy is given as H=10.2 cm.
Step 2: Calculate the height of the conical part
The height of the cone can be calculated by subtracting the radius of the hemisphere from the total height of the toy:
h=H−r=10.2cm−4.2cm=6cm
Step 3: Calculate the volume of the hemisphere
The volume Vh of a hemisphere is given by the formula:
Vh=23πr3
Substituting the value of r:
Vh=23π(4.2)3
Calculating (4.2)3:
(4.2)3=74.088
Now substituting back:
Vh=23π(74.088)≈148.1763π≈49.392πcm3
Step 4: Calculate the volume of the cone
The volume Vc of a cone is given by the formula:
Vc=13πr2h
Substituting the values of r and h:
Vc=13π(4.2)2(6)
Calculating (4.2)2:
(4.2)2=17.64
Now substituting back:
Vc=13π(17.64)(6)=13π(105.84)≈35.28πcm3
Step 5: Calculate the total volume of the toy
The total volume V of the wooden toy is the sum of the volumes of the hemisphere and the cone:
V=Vh+Vc=49.392π+35.28π=(49.392+35.28)π≈84.672πcm3
Calculating 84.672π:
V≈84.672×3.14≈266.112cm3
Final Answer
The volume of the wooden toy is approximately 266.112cm3.
---
- The radius of the hemisphere (and cone) is given as r=4.2 cm.
- The total height of the toy is given as H=10.2 cm.
The height of the cone can be calculated by subtracting the radius of the hemisphere from the total height of the toy:
h=H−r=10.2cm−4.2cm=6cm
The volume Vh of a hemisphere is given by the formula:
Vh=23πr3
Substituting the value of r:
Vh=23π(4.2)3
Calculating (4.2)3:
(4.2)3=74.088
Now substituting back:
Vh=23π(74.088)≈148.1763π≈49.392πcm3
The volume Vc of a cone is given by the formula:
Vc=13πr2h
Substituting the values of r and h:
Vc=13π(4.2)2(6)
Calculating (4.2)2:
(4.2)2=17.64
Now substituting back:
Vc=13π(17.64)(6)=13π(105.84)≈35.28πcm3
The total volume V of the wooden toy is the sum of the volumes of the hemisphere and the cone:
V=Vh+Vc=49.392π+35.28π=(49.392+35.28)π≈84.672πcm3
Calculating 84.672π:
V≈84.672×3.14≈266.112cm3
The volume of the wooden toy is approximately 266.112cm3.
Topper's Solved these Questions
Similar Questions
A cylindrical tub if radius 5cm and length 9.8cm is full of water .A splid in the form of a right circular cone mounted on a hemisphere is immersed into the tub.If the radius of the hemisphere is 3.5cm and the total height of the solid ids 8.5cm ,find the volume of water left in the tub
View SolutionA solid is in the shape of a cone surmounted on a hemi-sphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π=22/7 )
View SolutionA solid cylinder of diameter 12cm and height 15cm is melted and recast into toys with the shape of a right circular cone mounted on a hemisphere of radius 3cm. If the height of the toy is 12cm, find the number of toys so formed.
View SolutionA solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 3.5cm and the height of the cone is 4cm. The solid is placed in a cylindrical tub, full of water, in such a way that the whole solid is submerged in water. If the radius of the cylinder is 5cm and its height is 10.5cm, find the volume of water left in the cylindrical tub. (Useπ=227)
View SolutionA solid wooden toy is in the form of a hemisphere surmounted by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 16656cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs. 10 per cm2
View SolutionA toy is in the form of a cone mounted on a hemisphere of same radius 7 cm. If the total height of the toy is 31cm, find the total surface area.
View SolutionA toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm find the total surface area and volume of the toy.
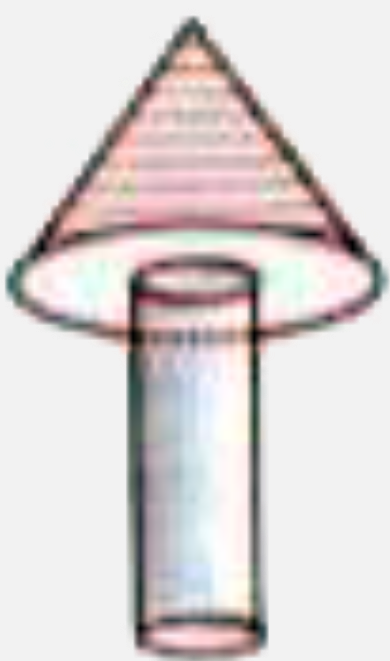
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside.
If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm, find the total surface area of the toy. Take π=3.14]
 View Solution
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside If the height of the cone is 24 cm the total height of the toy is 60 cm and the radius of the base of the cone= twice the radius of the base of the cylinder = 10 cm .Find the total surface area of the you.
 View Solution
View SolutionA toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
View Solution

