A square dart board is placed in the first quadrant from x=0 to x=6 and y=0 to y=6. A triangular region on the dart board is enclosed by y = 2, x = 6 and y = x. Find the probability that a dart that randomly hits the dart board will land in the triangular region formed by the three lines.
Area of square board =(6)2=36 sq. units
Now, DE=6−2=4units
BD = 6-2=4 uints
∴ Area of △BDE=12×DE×BD=12×4×4
= 8 sq. units
Hence, required probability =Area of △BDEArea of square OABC
=86×6=29

Topper's Solved these Questions
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Problems From NCERT /exemplar
10 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Exercise
29 Videos
- POLYNOMIALSBOOK - NAGEEN PRAKASHANCHAPTER - POLYNOMIALSEXERCISE - Revision Exercise Long Answer Questions
4 Videos
- QUADRATIC EQUATIONSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRATIC EQUATIONSEXERCISE - Revision Exercise Long Answer Questions
6 Videos
Similar Questions
A square dart board is placed in the first quadrant from x=0 to x=6 and y=0→y=6 . A triangular region on the dart board is enclosed by the lines y=2,x=6andy=x. Find the probability that a dart that randomly hits the dart board will land in the triangular region formed by the three lines.
View Solutionx−y=0,2x+y=6,x+2y=3 triangle formed by these lines is
View Solution
Knowledge Check
Find the area (in sq units) enclosed by y = 0, x+6=0 and 2x-3y=6.
A9B16C20D27Let S be the area of the region enclosed by y=e−x^2,y=0,x=0,andx=1. Then S≥1e (b) S≥1=1e S≤14(1+1√e) (d) S≤1√2+1√e(1−1√2)
AS≥1eBS≥1−1eCS≤14(1+1√e)DS≤1√2+1√e(1−1√2)Let S be the area of the region enclosed by y=e−x^2,y=0,x=0,andx=1. Then S≥1e (b) S≥1=1e S≤14(1+1√e) (d) S≤1√2+1√e(1−1√2)
AS≥1eBS≤1eCS≤14(1+1√e)DS≤14(1−1√2)
Find the area of the region in the first quadrant enclosed by x=y2andx=y+2
View SolutionIn the adjoining figure a dart is thrown at the dart board and lands in the interior of the circle . What is the probability that the dart will land in the shaded region.
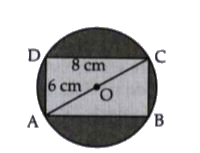
View SolutionDraw the graph of the following equations and answer the following questions :
x+y=5 x−y=5
(i) Find the solution of the equation from the graph.
(ii) Shade the triangular region formed by the lined and the y-axis.
View SolutionFind the area of the region bounded by y2=8x,x=2,x=4 and the x-axis in the first quadrant.
View SolutionSketch the region lying in the first quadrant and bounded by y=4x2 ,x = 0, y = 2 and y = 4. Find the area of the region using integration.
View Solution
