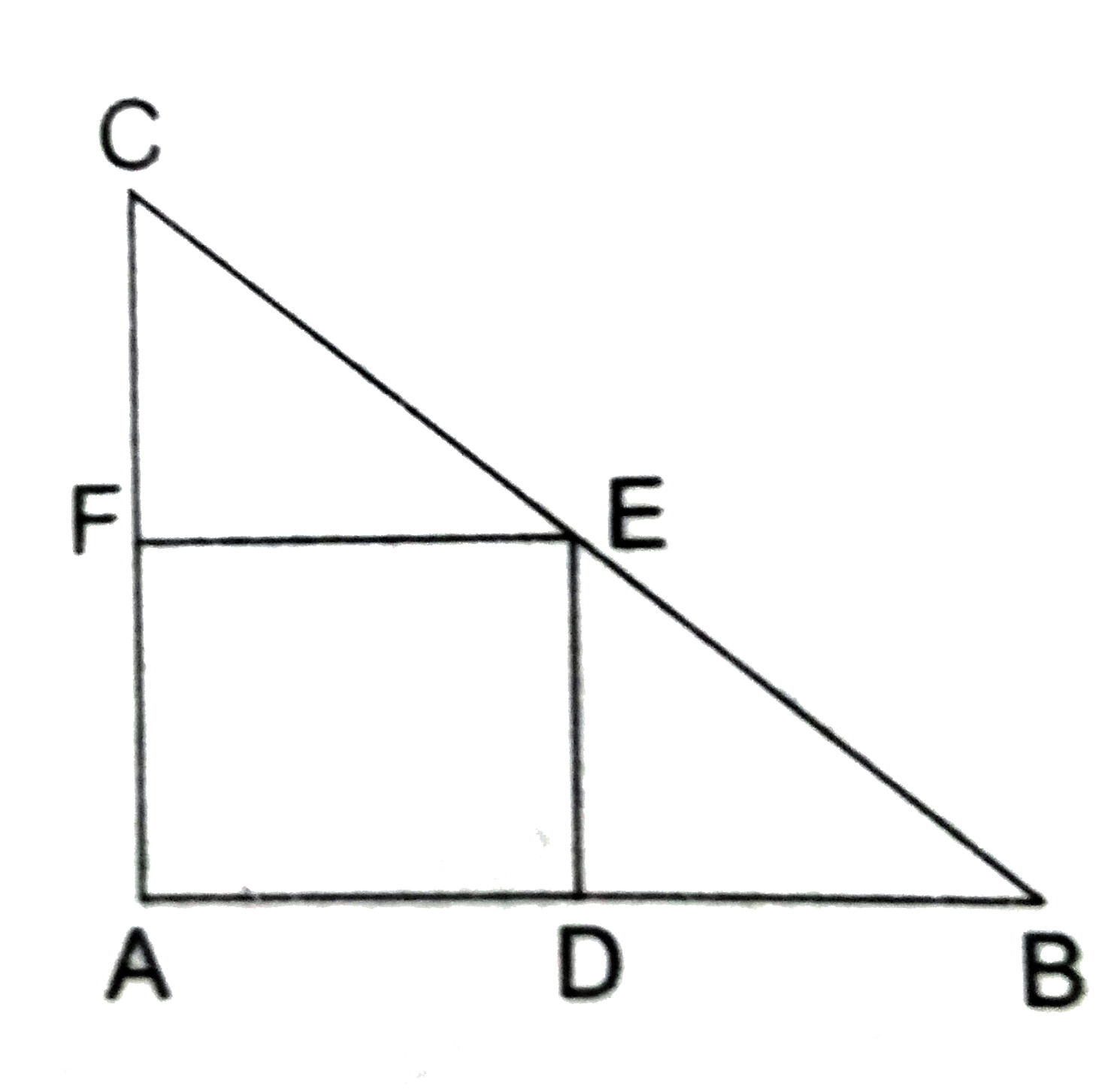
A square is inscribed in an isosceles right triangle so that the square and the triangle have an angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse
AB=ACandAD=AF⇒AB−AD=AC−AF⇒DB=CF.
We have △EFC≅△EDB [∵CF=DB,∠EFC=∠EDB=90∘,EF=ED].
∴CE=EB (c.p.c.t.).
Similar Questions
A square is incribed in an isoceles right triangle, so that the square and the triangle have one angle common. Show that the vertex of the sqare opposite the vertex of the common angle bisects the hypotenuse.
View SolutionA square is inscribed in a right-angled triangle with legs p and q, and has a common right angle with the triangle. The diagonal of the square is given by
View Solution
Knowledge Check
- Question 1 - Select One
The hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
A5 cm2B6.25 cm2C6.5 cm2D12.5 cm2
A side of an isosceles right angled triangle is x. Find its hypotenuse.
View SolutionAn isosceles right-angled triangle has area 2 square unit. What is its perimeter ?
View SolutionIn an isosceles triangle,the base angles are equal.The vertex angle is thrice either base angle. What are the measures of the angles?
View SolutionThe vertex angle of an isosceles triangle is 80∘ , Find ot the measure of base angles .
View SolutionIn an Isosceles triangle the base angles are equal and the vertex angle is twice of each base angle. Find the measures of the angles of the triangle.
View SolutionIn an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
Let each base angle be x in an isosceles △ABC
Then vertex angle be 2(x+x)=4x
Since sum of angles of a triangle is 1800
Hence,4x+x+x=1800
6x=1800
⇒x=300
Angles are 300,300,1200View SolutionIn an isosceles triangle if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle
View Solution

