A square of n units is divided into n2 squares each of area 1 sq unit. Find the number of ways in which 4 points (out of (n+1)2 vertices of the squares) can be chosen so that they form the vertices of a square.Solution in Punjabi
The correct Answer is:n2(n+1)2
Step by step video & image solution for A square of n units is divided into n^(2) squares each of area 1 sq unit. Find the number of ways in which 4 points (out of (n+1)^(2) vertices of the squares) can be chosen so that they form the vertices of a square. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)28videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Statement I And Ii Type Questions)12videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT MATHSCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)35videos
PARABOLA
- BOOK - ARIHANT MATHSCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)55videos
PROBABILITY
Similar Questions
There is a rectangular sheet of dimension (2m−1)×(2n−1), (where m>0,n>0) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
05:19View SolutionStatement-1: The smallest positive integer n such that n! can be expressed as a product of n-3 consecutive integers, is 6.
Statement-2: Product of three consecutive integers is divisible by 6.05:45View SolutionLet A and B be two finite sets such that n(A) =85, n(B) = 65and n(A ∪ B) = 135, find n(A ∩ B)?
View Solutionfind the derivative of sin x cos x
00:56View SolutionA rectangle with sides of lengths (2n-1) and (2m-1) units is divided into squares of unit length.The number of rectangles which can be formed with sides of odd length,is (a) m^(2)n^(2) (b) mn(m+1)(n+1) (c) 4^(m+n-1) (d) non of these
02:39View SolutionArea of square ABCD is 4 unit^2 *M and N are mid points of AB and BC. Find PC.
03:36View SolutionFind the value of k so that the area of the triangle with vertices (1,−1),(−4,2k)and(−k,−5) is 24 square units.
04:57View SolutionThe ratio of the areas of two squares is 1:4 .if the area of the first is 9 sq. units . The area of the first square is ____ ( in sq. units)
04:15View SolutionIf the points ( k, k -1) , (k + 2 , k + 1) and (k , k +3) are three consective vertices of a square , then its area (in square units ) is _______.
02:22View SolutionThe area of a square with one of its vertices as (5 , -2) and the mid-points of the diagonals (3,2) is _______. (in sq. units)
06:56View Solution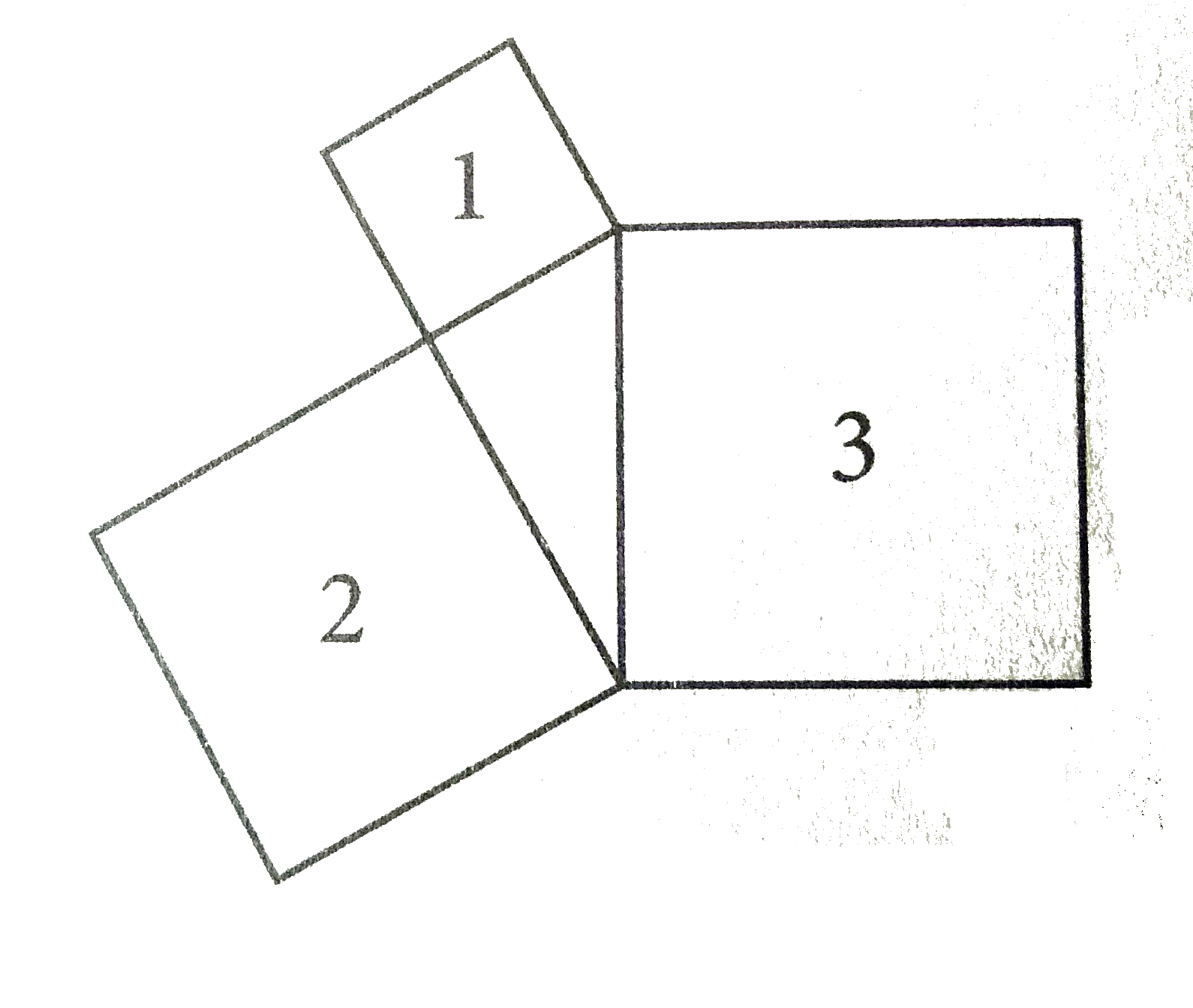
Each of the quadrilaterals figure above is a square. The area of the smallest square (square 1) is 16 square units, and the area of the medium square (square 2) is 48 square units. What is the area, in square units, of the largest square (square 3)?02:46View SolutionIf area of ΔABC is 12 square units and vertices are A(x,2), B(4,−1) and C(−3,7) , then find the value of x.
05:53View SolutionThe area of paper can be divided into 144 squares, but if the dimensions of each square, were reduced by 2 cm each, then the number of squares so formed are 400. The area of the paper initially was :
01:29View SolutionShow that the points (1, 7), (4, 2), (−1, −1) and (−4, 4) are the vertices of a square.
02:56View Solution
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
The value of α for which side of nth square equal to the diagonal of (n+1)th square is06:48View SolutionShow that the points (1,7),(4,2),(−1,−1)and(−4,4) are the vertices of a square.
05:31View Solution