A student appears for tests I, II and III. The student is successful if he passes either in tests I and II or tests I and III. The probabilities of the student passing in tests I, II, and III are, respectively, p, q, and 1/2. then p(1+q)=
1/2
1
3/2
3/4
The correct Answer is:B
To solve the problem, we need to find the value of p(1+q) given the probabilities of passing tests I, II, and III as p, q, and 12 respectively.
1. Define Events: Let A, B, and C represent the events of passing tests I, II, and III respectively. The probabilities are:
- P(A)=p
- P(B)=q
- P(C)=12
2. Successful Conditions: The student is successful if he passes either:
- Tests I and II (events A and B)
- Tests I and III (events A and C)
Therefore, the successful event can be represented as:
P(Success)=P(A∩B)+P(A∩C)
3. Calculate Probabilities:
- The probability of passing both tests I and II:
P(A∩B)=P(A)⋅P(B)=p⋅q
- The probability of passing both tests I and III:
P(A∩C)=P(A)⋅P(C)=p⋅12
4. Combine Probabilities:
P(Success)=P(A∩B)+P(A∩C)=pq+p⋅12
5. Set Up the Equation: Since the student is successful if he passes either of the conditions, we can express this as:
P(Success)=pq+p2
6. Total Probability of Success: The total probability of success must equal the probability of passing at least one of the tests. The probability of passing at least one of the tests can be calculated as:
P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)
However, since we are only interested in the successful conditions defined earlier, we can simplify our approach.
7. Equating to 1: From the problem, we can set the successful probability equal to 1:
pq+p2=1
8. Rearranging the Equation:
pq+p2=1⟹p(1+q)=1
9. Final Result: Thus, we find:
p(1+q)=1
Conclusion:
The value of p(1+q) is 1.
- P(A)=p
- P(B)=q
- P(C)=12
- Tests I and II (events A and B)
- Tests I and III (events A and C)
P(Success)=P(A∩B)+P(A∩C)
- The probability of passing both tests I and II:
P(A∩B)=P(A)⋅P(B)=p⋅q
- The probability of passing both tests I and III:
P(A∩C)=P(A)⋅P(C)=p⋅12
P(Success)=P(A∩B)+P(A∩C)=pq+p⋅12
P(Success)=pq+p2
P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)
However, since we are only interested in the successful conditions defined earlier, we can simplify our approach.
pq+p2=1
pq+p2=1⟹p(1+q)=1
p(1+q)=1
The value of p(1+q) is 1.
Topper's Solved these Questions
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CHOICE ANSWER TYPE
17 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - LINKED COMPREHENSION TYPE
43 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - CONCEPT APPCICATION EXERCISE 14.6
5 Videos
- PROBABILITY I BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - JEE Advanced
7 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Video
Similar Questions
A student appears for tests I, II and III. The student is considered successful if he passes in tests I, II or III or all the three. The probabilities of the Student passing in tests I,II and III are m, n and 12 respectively. If the probability of the student to be successful is 12, then which one of the following is correct? (a) m(1+n)=1 (B) n(1+m)=1 (C) m=1 (D) mn=1
View SolutionIn a class, 70 students wrote two tests wiz, test-I and test-II 50% of the students failed in test I and 40% of the students in test -II. How many students passed in both tests?
View Solution
Knowledge Check
If 95% students pass the test , it mean 5% students get less than minimum passing maeks . Hence the minimum passing mark is
AD5BQ2CP5DP95
In a test. 90% of the students passed and 4 students failed. How many students appeared for the test?
View SolutionIn a class of 85% students pass in a surprise test. What per cent of students did not pass?
View SolutionIn a college, 70% students pass in Physics, 75% pass in Mathematics and 10% students fail in both. One student is chosen at random. What is the probability that
(i) He passes in Physics and Mathematics
(ii) He passes in Mathematics given that he passes in Physics
(iii) He passes in Physics given that he passes in Mathematics.
View SolutionUse graph paper for this question.
The amrks obtained by 120 students in an English test are given below :
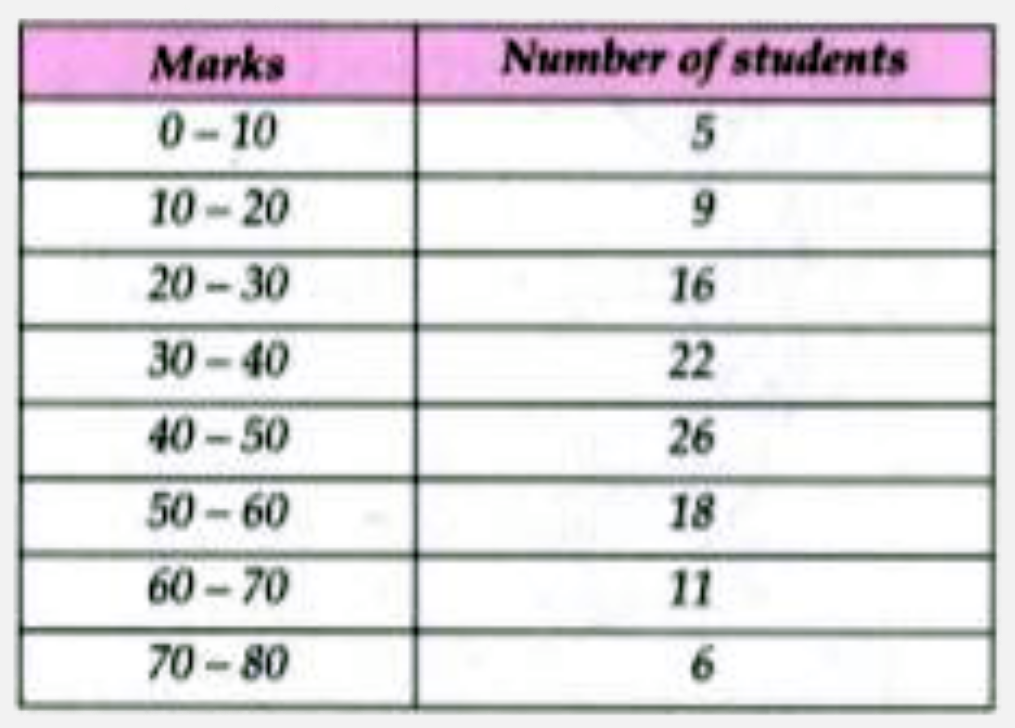

Draw the ogive and hence, estimate :
the number of students who did not pass test if the pass percetage was 50.
View SolutionComment on the following figure: I, II and III, A, B, C, D, G, P, Q, R, S are species.

View SolutionA probability of student A passing an examination is 2/9 and of student B passing is 5/9. Assuming the two events: A passes, B passes as independent, find the probability of : (i) only A passing the examination (ii) only one of them passing the examination.
View SolutionRefer to Table 14.7, Chapter 14.(i) Find the probability that a student obtained less than 20% in the mathematics test.(ii) Find the probability that a student obtained marks 60 or above.
View Solution