A survey was conducted among 300 students. If was found that 125 students like play cricket, 145 students like to play football and 90 students like to play tennis, 32 students like to play exactly two games out of the three games.
How many students like to play all the three games?
14
21
28
35
The correct Answer is:A
To solve the problem, we need to determine how many students like to play all three games: cricket, football, and tennis. We will use the principle of inclusion-exclusion.
1. Define the Sets:
- Let A be the set of students who like cricket.
- Let B be the set of students who like football.
- Let C be the set of students who like tennis.
From the problem, we have:
- |A|=125
- |B|=145
- |C|=90
2. Total Students:
- The total number of students surveyed is 300.
3. Using the Inclusion-Exclusion Principle:
- According to the principle, the total number of students can be expressed as:
|A∪B∪C|=|A|+|B|+|C|−|A∩B|−|B∩C|−|A∩C|+|A∩B∩C|
- We know that |A∪B∪C|=300.
4. Substituting Known Values:
- We also know that 32 students like exactly two games. This means:
|A∩B|+|B∩C|+|A∩C|−3|A∩B∩C|=32
- Let x=|A∩B∩C| (the number of students who like all three games).
5. Setting Up the Equations:
- From the inclusion-exclusion principle:
300=125+145+90−(|A∩B|+|B∩C|+|A∩C|)+x
- This simplifies to:
300=360−(|A∩B|+|B∩C|+|A∩C|)+x
- Rearranging gives:
|A∩B|+|B∩C|+|A∩C|=60+x(Equation 1)
6. Using the Second Equation:
- From the second equation about students liking exactly two games:
|A∩B|+|B∩C|+|A∩C|−3x=32(Equation 2)
7. Substituting Equation 1 into Equation 2:
- Substitute |A∩B|+|B∩C|+|A∩C| from Equation 1 into Equation 2:
(60+x)−3x=32
- This simplifies to:
60−2x=32
- Rearranging gives:
2x=60−32=28
- Thus, we find:
x=14
8. Conclusion:
- Therefore, the number of students who like all three games is 14.
Final Answer:
The number of students who like to play all three games is 14.
- Let A be the set of students who like cricket.
- Let B be the set of students who like football.
- Let C be the set of students who like tennis.
From the problem, we have:
- |A|=125
- |B|=145
- |C|=90
- The total number of students surveyed is 300.
- According to the principle, the total number of students can be expressed as:
|A∪B∪C|=|A|+|B|+|C|−|A∩B|−|B∩C|−|A∩C|+|A∩B∩C|
- We know that |A∪B∪C|=300.
- We also know that 32 students like exactly two games. This means:
|A∩B|+|B∩C|+|A∩C|−3|A∩B∩C|=32
- Let x=|A∩B∩C| (the number of students who like all three games).
- From the inclusion-exclusion principle:
300=125+145+90−(|A∩B|+|B∩C|+|A∩C|)+x
- This simplifies to:
300=360−(|A∩B|+|B∩C|+|A∩C|)+x
- Rearranging gives:
|A∩B|+|B∩C|+|A∩C|=60+x(Equation 1)
- From the second equation about students liking exactly two games:
|A∩B|+|B∩C|+|A∩C|−3x=32(Equation 2)
- Substitute |A∩B|+|B∩C|+|A∩C| from Equation 1 into Equation 2:
(60+x)−3x=32
- This simplifies to:
60−2x=32
- Rearranging gives:
2x=60−32=28
- Thus, we find:
x=14
- Therefore, the number of students who like all three games is 14.
The number of students who like to play all three games is 14.
Topper's Solved these Questions
Similar Questions
In a class of 35 students, 24 like to play cricket and 16 like to play football. Also, each student likes to play at least one of the two games. How many students like to play both cricket and football?
View SolutionIn a class of 35 students, 24 like to play cricket and 16 like to play football. Also, each student likes to play at least one of the two games. How many students like to play both cricket and football?
View Solution
Knowledge Check
A survey was conducted among 300 students. It was found that 125 students like to play cricket. 145 students like to play football and 90 students like to play tennis, 32 students like to play exactly two games out of the three games.
How many students like to play all three games?A14B21C28D35A survey was conducted among 300 students. It was found that 125 students like to play cricket. 145 students like to play football and 90 students like to play tennis, 32 students like to play exactly two games out of the three games.
How many students like to play all three games?A196B228C254D268In a class of 60 students , 25 students play cricket and 20 students play tennis and 10 students play both the games. Find the number of students who play neither.
A25B35C40D15
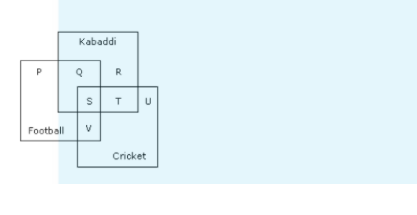
In the following Venn diagram the total number of students who play all the three games is:
View SolutionIn a class of 40 students, 24 like to play guitar and 25 like to play piano. If each students like at least one of the musical instrutment, then how many like to play both piano and guitar?
View SolutionIn a class of 35 students, 24 students like cricket and 16 like football. If each student plays atleast one game, find how many students like both games ?
View SolutionIn a class of 65 students , 30 students play cricket and 20 students play tennis and 10 students play both the games Then , the number of students who play neither is :
View SolutionA class has 50 student ,each student likes either cricket or football or both .Sixteen students like both the games .Find the number of students who like exactly one game .
View Solution
