A swimmer S is in the sea at a distance dkm from the closest point A on a straight shore. The house of the swimmer is on the shore at distance Lkm /h per hour and walk at a speed of vkm/h , u<v . At what point on the shore should he land so that he reaches his house in the shortest possible time?
Step by step video & image solution for A swimmer S is in the sea at a distance dk m from the closest point A on a straight shore. The house of the swimmer is on the shore at distance Lk m /h per hour and walk at a speed of vk m//h , u<v . At what point on the shore should he land so that he reaches his house in the shortest possible time? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A swimmer S is in the sea at a distance dkm from the closest point A on a straight shore. The house of the swimmer is on the shore at distance Lkm from A. He can swin at speed oh ukm/h. walk at speed at vkm/h. At what point on shore should he land so that hhe reaches his house in the shortest time.
View SolutionThe distance (in km) travelled in h hours at a constant speed of 40 km per hour is
View Solution
Knowledge Check
If the distance of 200 m is covered in 20 s, then the speed is
A10 km/hB20 km/hC26 km/hD36 km/hA swimmer swims in still water at a speed =5km/hr. He enters a 200m wide river, having river flow speed =4km/hr at point A and proceeds to swim at an angle of 127∘(sin37∘=0.6) with the river flow direction. Another point B is located directly across A on the other side. the swimmer lands on the other bank at a point C, form which he walks the distance CB with a speed =3km/hr. The total time in which he reaches from A to B is
A5minutesB4minutesC3minutesDNoneA swimmer start swimming from a sea shore in south direction and other one in east direction. Their distance becomes 100 km. in 2 hrs. If speed of one swimmer is 75% of another swimmer, find the speed of swimmer who swims faster ?
A30 km./hr.B40 km./hr.C45 km./hr.D60 km./hr.
Two swimmers leave point A on the bank of the river to reach point B lying right across on the other bank. One of them crosses the river along the straight line AB while the other swims at right angles to the stream and then walks the distance that he has been carried away by the stream to get to point B. What was the velocity u of his walking if both swimmers reached the destination simultaneously? The stream velocity v0=2.0km/hour and the velocity v′ of each swimmer with respect to water equals to 2.5km per hour.
View SolutionTwo swimmers leave point A on one bank of the river to reach point B lying right across on the other bank. One of them crosses the river along the straight line AB while the other swims at right angles to the stream and them walks the distance that he has been carried by the stream to get to point B. what was the velocity v0 of his walking if both swimmers reach the destination simultaneously? The stream velocity is u and v is the velocity of swimmer in still water.
View SolutionTwo swimmers start at the same time from point A one bank of a river to reach point B on the other bank, lying directly oppostie to point A. one of them crosses the river along the straight line AB, while the other swims at right angles to the stream and then walks the distance, which he has been carried awayby the stream to get to point B. Both swimmers reach point B at the same time. what was the velocity (assumed uniform) of his walking if velocity of both the swimmers in still water is 2.5 km h−1 and the stream velocity is 2 km h−1?

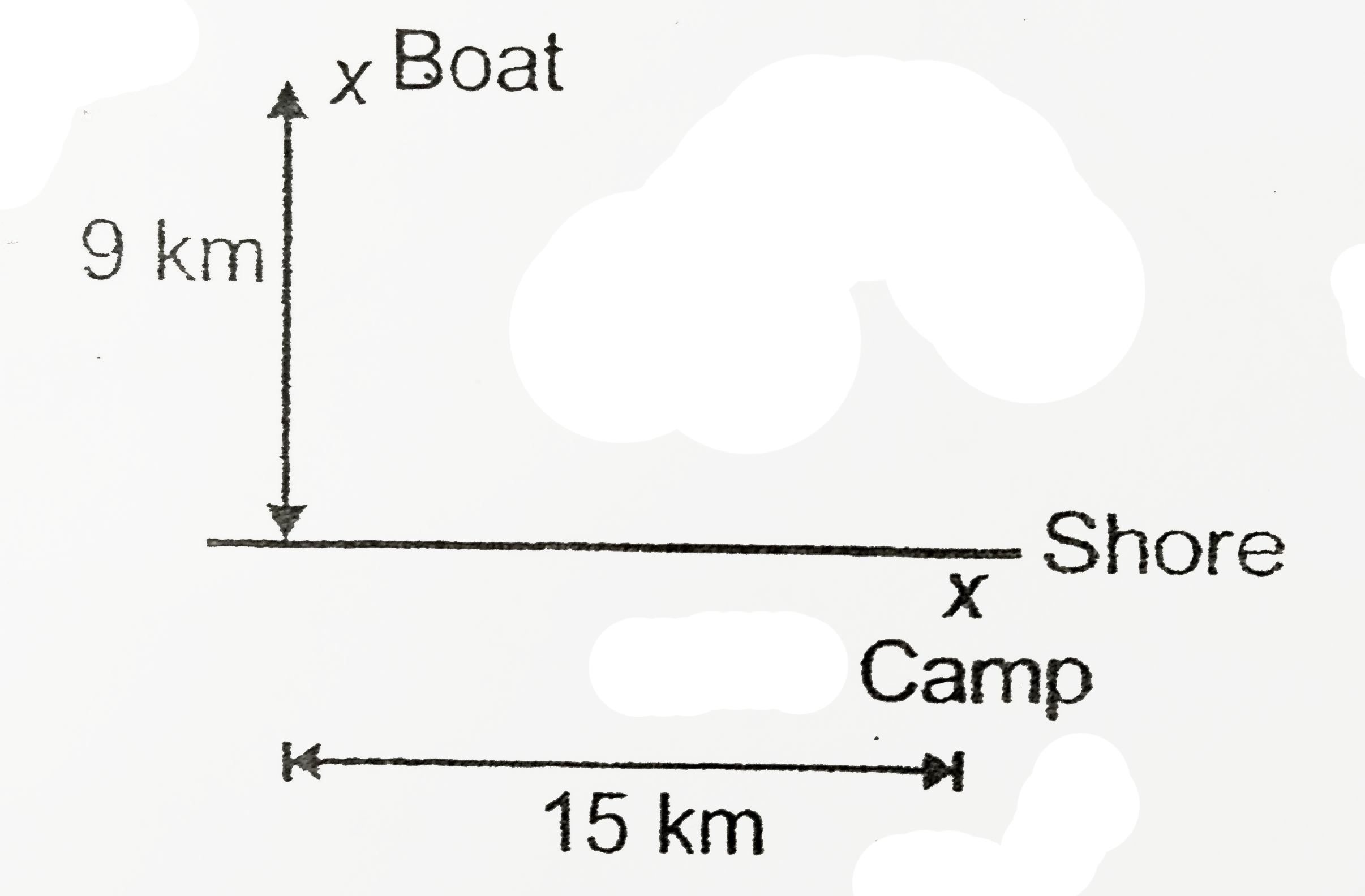
View SolutionA fishing boat is anchored 9 km away from the the nearest point on the shore. A messanger must be sent from the fishing boat to a camp, 15 km from the point on shore closest to boat. If the messanger can walk at a speed of 5 km per hour and can row at 4 km/h. determine the distance of that point (in km) from the shore, where he must land so as to reach the shore in least possible time.
View SolutionA wooden log of mass 120kg is floating on still water perpendicular to the shore. A man of mass 80kg is standing at the centre of mass of the log and he is at a distance of 30m from the shore. When he walks through a distance of 10m towards the shore and halts, now his distance from the shore is
(A) 20m (B) 24m (C) 26m (D) 28m
View Solution
