Question

A tangent is drawn to each of the circles $x^2+y^2=a^2$
and $x^2+y^2=b^2\stackrel{.}{}$
Show that if the two tangents are mutually perpendicular, the locus of
their point of intersection is a circle concentric with the given circles.

Explanation

In the figure, from variable point P(h,k) tangents PA and PB are drawn to two circles `x^(2)+y^(2)=a^(2)` and `x^(2)+y^(2)=b^(2)`. Tangents PA and PB are perpendicuarl .
Clearly, OAPB is a reactangle.
`:. OP ^(2)= OB^(2)+BP^(2)=h^(2)+k^(2)=a^(2)+b^(2)`

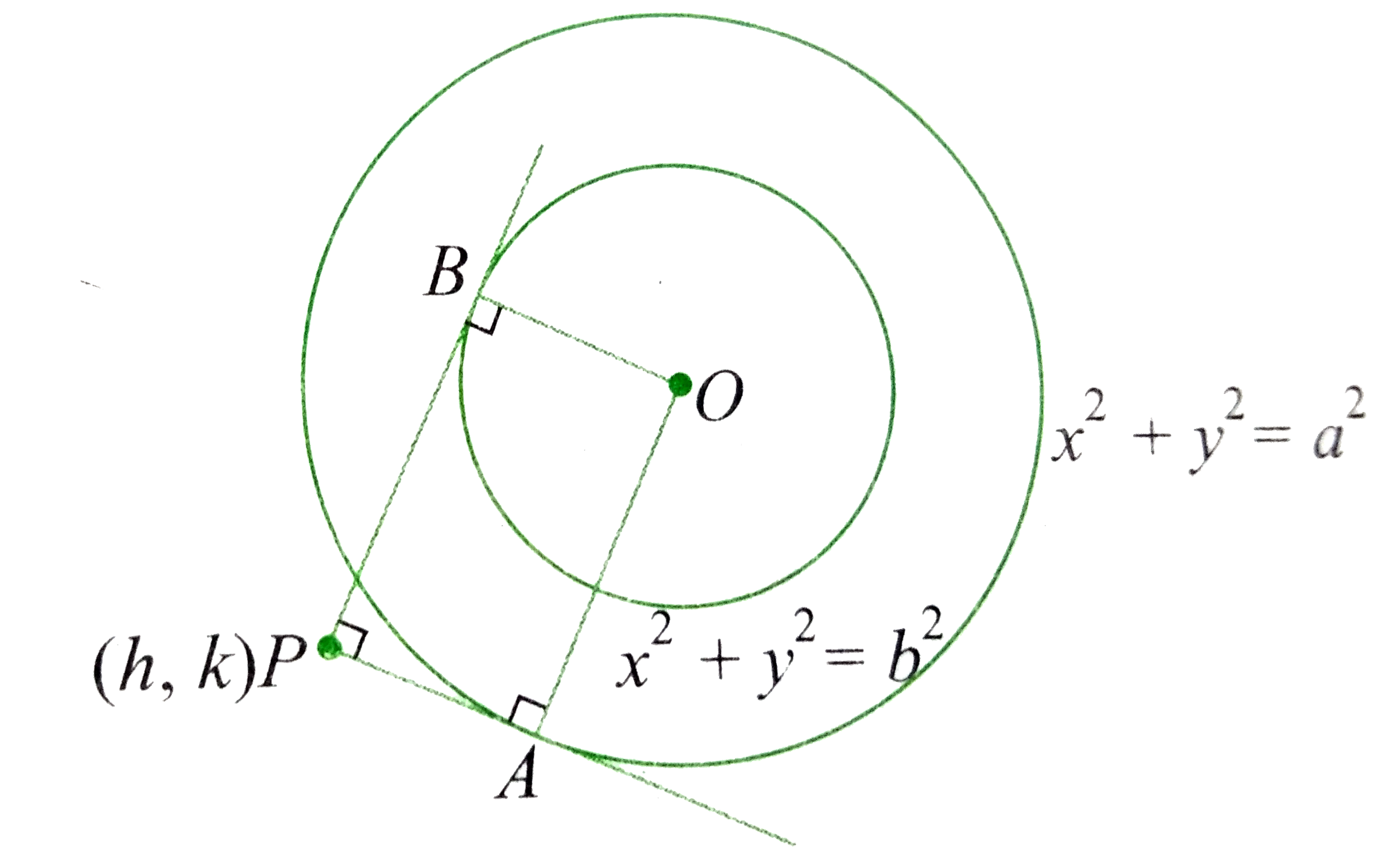
Therefore, required locus is `x^(2)+y^(2)=a^(2)+b^(2)`, which is concentric circle with given circles.