A toy was made by scopping out a hemisphere from each end of a solid cylinder . If the height of the cylinder is h cm and base radius is r rms . Find the total surface area of the toy . Solution in Kannada
Step by step video & image solution for A toy was made by scopping out a hemisphere from each end of a solid cylinder . If the height of the cylinder is h cm and base radius is r rms . Find the total surface area of the toy . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CPC MODEL QUESTION PAPER -6BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CPC MODEL QUESTION PAPER -6EXERCISE - QUESTION
30 Videos
- CO-ORDINATE GEOMETRYBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - EXERCISE 7.4
6 Videos
- CPC MODEL QUESTION PAPER 5BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CPC MODEL QUESTION PAPER 5EXERCISE - VI. Answer the following :
1 Videos
Similar Questions
What is the pq form of 43.¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯123456789?
View SolutionDetermine the ratio in which the line 2x + y - 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).

View SolutionA frustum of a cone has its radii of 15cm and 7cm with a height of 6cm is completely filled with water. Find the volume of water and curved surface area of frusturm ( Take π=3.14)
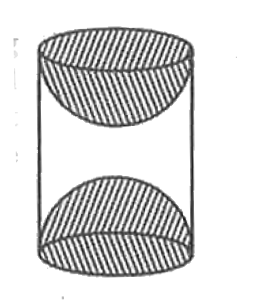
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 16.37. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base radius is 3.5 cm, find the total surface area of the article.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder ,as shown in Fig . If the height of the cylinder is 10 cm and its base is of radius 3.5cm, find the total surface area of the article.
View SolutionA toy is in the shape of a cylinder surmounted by a hemisphere . The height of the toy is 25 cm . Find the total surface area of the toy is its common diameter is 12 cm .
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its radius of the base is of 3.5 cm, find the total surface area of the article .

View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder. As shown in the given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm find the total surface area of the article.

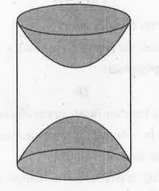
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. . If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, find the total surface area of the article.
View Solution
