A triangle ABC has vertices A(5,1),B(−1,−7)andC(1,4) respectively. L be the line mirror passing through C and parallel to AB and a light ray eliminating from point A goes along the direction of internal bisector of the angle A, which meets the mirror and BC at E, D respectively. If sum of the areas of △ACE and △ABE is K sq units then2K5−6 isSolution in Tamil
a. 17 sq. units
b. 18 sq. units
c. 503 sq. units
d. 20 sq. units
The correct Answer is:C
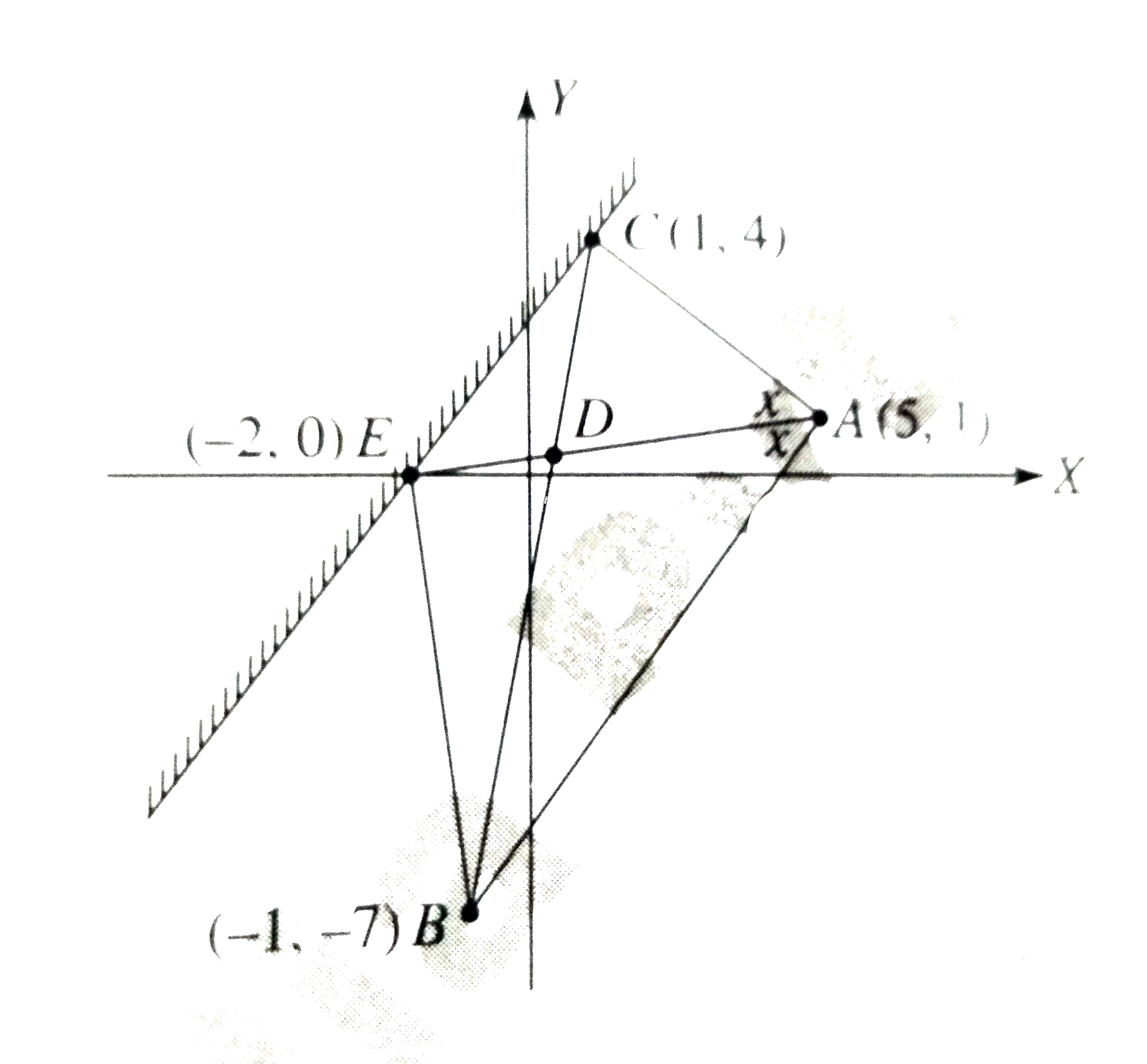
ADDE=BDDC=ABAC
∴ Point D(13,13) and E(−2,0).
Area of ΔADC+ Area of ΔBDE
=253+253
=503 sq. units
Topper's Solved these Questions
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Comprehension Type
4 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Question Bank
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main Previous Year
6 Videos
Similar Questions
A(x1,y1),B(x2,y2),C(x3,y3) are three vertices of a triangle ABC, lx+my+n=0 is an equation of line L. If L intersects the sides BC,CA and AB of a triangle ABC at P,Q,R respectively, then BPPC×CQQA×ARRB is equal to
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet f(x)=√x2+px+1x2−p. If f(x) is discontinuous at exactly 2 values of x then number of integers in the range of p is
View SolutionThe lines p(p2+1)x−y+q=0 and (p2+1)2x+(p2+1)y+2q=0 are perpendicular to a common line for
View SolutionA triangle ABC has vertices A(5, 1), B (-1, -7) and C(1, 4) respectively. L be the line mirror passing through C and parallel to AB and a light ray eliminating from point A goes along the direction of internal bisector of the angle A, which meets the mirror and BC at E, D respectively. If sum of the areas of triangle ACE and triangle ABE is K sq units then(2K)/5-6 is
View SolutionIn a triangle ABC, D and E are points on AB, AC respectively such that DE is parallel to BC. Suppose BE, CD intersect at O. If the areas of the triangles ADE and ODE are 3 and 1 respectively, find the area of the triangle ABC, with justification
View Solutionएक ΔABC के ∠B और ∠Cके समद्विभाजक सम्मुख AC और AB को क्रमशः बिंदु D और E पर काटते है|यदि DE∣∣BC हो, तो सिद्ध करों की ΔABC एक समद्विबाहु त्रिभुज है|
View SolutionA(0,0),B(4,2)andC(6,0) are the vertices of the triangle ABC . BD is an altitude of triangle ABC . A line passes through D and parallel with AB meets BC at E . Then the product of the area (in sq. units ) of ΔABCandΔBDE will be -
View SolutionΔABC के शीर्ष A(4, 6), B(1, 5) और C(7, 2) हैं । एक रेखा, AB और AC को क्रमश: D और E पर इस प्रकार काटती है कि ADAB=AEAC=14 है । ΔADE का क्षेत्रफल ज्ञात कीजिए और इसकी तुलना ΔABC के क्षेत्रफल से कीजिए ।
View SolutionΔABC లో DE // BC మరియు D, E లు వరుసగా AB, AC లపై బిందువులైన
View SolutionThe vertices of a Δ ABC are A (4,6), B (1, 5) and C (7,2). A line is drawn to intersect sides AB and AC at D and E respectively, such that ADAB=AEAC=14. Calculate the area of Δ ADE and compare it with area of Δ ABC
View SolutionA triangle ABC has vertices A(5,1),B(−1,−7)andC(1,4) respectively. L be the line mirror passing through C and parallel to AB and a light ray eliminating from point A goes along the direction of internal bisector of the angle A, which meets the mirror and BC at E, D respectively. If sum of the areas of △ACE and △ABE is K sq units then2K5−6 is
View SolutionInternal bisector of an angle ∠A of triangle ABC meets side BC at D. A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent the sides of DABC then
View SolutionThe side AC of a triangle ABC is produced to point E so that CE=12 AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
3DF=EF
View SolutionThe side AC of a triangle ABC is produced to point E so that CE=12 AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
4CR=AB
View Solution
