A triangle ABC is right angled at B, find the value of secA.sinC−tanA−tanCsinB
The correct Answer is:0
To solve the problem, we need to find the value of the expression (secA⋅sinC−tanA−tanC)/sinB for a right-angled triangle ABC, where the right angle is at B.
1. Identify the Angles and Sides:
In triangle ABC, angle B is the right angle. Therefore, angles A and C are complementary, meaning A+C=90∘.
2. Recall Trigonometric Identities:
- secA=1cosA=HypotenuseBase
- sinC=Opposite to CHypotenuse
- tanA=Opposite to ABase
- tanC=Opposite to CBase
3. Assign Variables:
Let:
- Hypotenuse = Z
- Base (adjacent to angle A) = X
- Opposite to angle A = Y
4. Calculate Each Trigonometric Function:
- secA=ZX
- sinC=YZ
- tanA=YX
- tanC=XY
5. Substitute Values into the Expression:
Substitute the values of secA, sinC, tanA, and tanC into the expression:
secA⋅sinC−tanA−tanCsinB
becomes:
(ZX⋅YZ)−YX−XYsinB
6. Simplify the Expression:
The expression simplifies to:
YX−YX−XYsinB
Since sinB=1 (because angle B is 90∘):
=−XY1=−XY
7. Final Result:
Thus, the value of the expression is:
−XY
In triangle ABC, angle B is the right angle. Therefore, angles A and C are complementary, meaning A+C=90∘.
- secA=1cosA=HypotenuseBase
- sinC=Opposite to CHypotenuse
- tanA=Opposite to ABase
- tanC=Opposite to CBase
Let:
- Hypotenuse = Z
- Base (adjacent to angle A) = X
- Opposite to angle A = Y
- secA=ZX
- sinC=YZ
- tanA=YX
- tanC=XY
Substitute the values of secA, sinC, tanA, and tanC into the expression:
secA⋅sinC−tanA−tanCsinB
becomes:
(ZX⋅YZ)−YX−XYsinB
The expression simplifies to:
YX−YX−XYsinB
Since sinB=1 (because angle B is 90∘):
=−XY1=−XY
Thus, the value of the expression is:
−XY
Topper's Solved these Questions
Similar Questions
A triangle ABC is right angled at B. Find the value of secA.sinC−tanA.tanCsinB
View SolutionA triangle ABC is right angled at B, find the value of
secA.cosecC−tanA.cotCsinB
View SolutionIf triangle ABC is right angled at C, then the value of sec (A+B) is
View SolutionIn triangle ABC, right-angled at B. if tanA=1√3find the value of:
(i) sinAcosC+cosAsinC
(ii) cosAcosCsinAsinC
View SolutionLet triangle ABC be right angled at C.If tanA+tanB=2, then-
View SolutionIn a right triangle ABC , right angled at C , if tanA=1 , then verify that 2sinAcosA=1 .
View Solution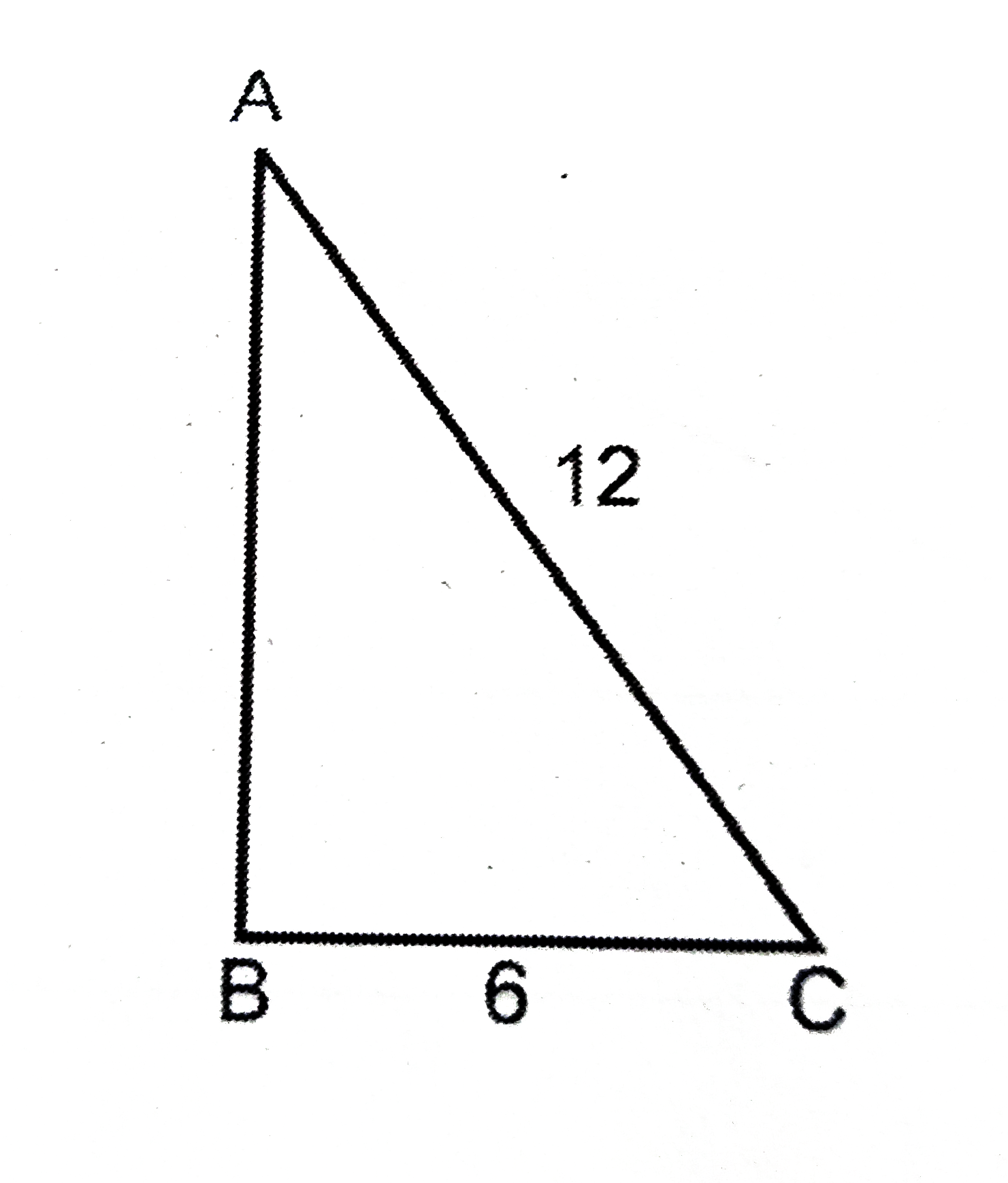
In the figure shown above, ABC is a triangle right angled at B. What is the value of angle A, in degrees?
View SolutionIf in a triangle ABC, right angled at B, s-a=3, s-c=2, then the values of a and c are respectively
View SolutionIn a right triangle ABC , right angled at B, the ratio of AB→AC is 1:√2 . Find the values of 2tanA1+tan2A and (ii) 2tanA1−tan2A
View SolutionThe perimeter of a triangle ABC right angled at C is 70 and the inradius is 6, then |a−b|=
View Solution
