A vertical pole PO is standing at the centre O of a square ABCD. If AC subtends an angle of 90∘ at the top , P of the pole, then the angle subtended by a side of the square at P is
45∘
30∘
60∘
none of these
The correct Answer is:C
To solve the problem step by step, let's break it down clearly.
Given:
- A vertical pole PO is standing at the center O of a square ABCD.
- The diagonal AC subtends an angle of 90° at the top P of the pole.
To Find:
- The angle subtended by a side of the square at P.
1. Understanding the Geometry:
- Let the side length of the square ABCD be A.
- The center O of the square divides the square into four equal parts.
- The diagonal AC of the square will have a length of AC=√2A (since the diagonal of a square is given by √2×side).
Hint: Remember the formula for the diagonal of a square.
2. Positioning the Points:
- Place the square ABCD in a coordinate system:
- A = (−A/2,A/2)
- B = (A/2,A/2)
- C = (A/2,−A/2)
- D = (−A/2,−A/2)
- O = (0,0) (the center of the square)
- P = (0,0,h) (the top of the pole at height h)
Hint: Visualize the square in a 3D coordinate system to understand the positions of points.
3. Using the Given Angle:
- The angle subtended by the diagonal AC at point P is given as 90°.
- This means that the lines PA and PC create a right triangle with the diagonal AC.
Hint: Recall that in a right triangle, the angles opposite the equal sides are equal.
4. Finding the Angles at P:
- Since the angle subtended by AC at P is 90°, the angles ∠AOP and ∠COP are both 45° (because the diagonal bisects the angle at the center).
Hint: Use the property of angles in an isosceles triangle.
5. Finding the Lengths:
- The distance OA (from O to A) is A√2 (half the diagonal).
- The height of the pole is h, so we can use the Pythagorean theorem in triangle AOP:
AP2=AO2+OP2
AP2=(A√2)2+h2
AP2=A22+h2
Hint: Use the Pythagorean theorem to relate the sides of the triangle.
6. Considering the Side of the Square:
- Now, consider the triangle ABP, where AB is a side of the square.
- Since OA = OB, the angle subtended by side AB at P will also be equal to the angle subtended by AC.
Hint: Use symmetry in the square to relate angles.
7. Calculating the Angle:
- Since triangle APB is isosceles (AP = PB), we can find the angle α subtended by side AB at P.
- The angles at P will be equal, and since the total angle around point P is 360°, we can deduce:
α+α+90°=180°
2α=90°
α=45°
Hint: Use the sum of angles in a triangle to find the unknown angle.
8. Conclusion:
- Therefore, the angle subtended by a side of the square at point P is 45°.
Final Answer:
The angle subtended by a side of the square at P is 45°.
- A vertical pole PO is standing at the center O of a square ABCD.
- The diagonal AC subtends an angle of 90° at the top P of the pole.
- The angle subtended by a side of the square at P.
- Let the side length of the square ABCD be A.
- The center O of the square divides the square into four equal parts.
- The diagonal AC of the square will have a length of AC=√2A (since the diagonal of a square is given by √2×side).
- Place the square ABCD in a coordinate system:
- A = (−A/2,A/2)
- B = (A/2,A/2)
- C = (A/2,−A/2)
- D = (−A/2,−A/2)
- O = (0,0) (the center of the square)
- P = (0,0,h) (the top of the pole at height h)
- The angle subtended by the diagonal AC at point P is given as 90°.
- This means that the lines PA and PC create a right triangle with the diagonal AC.
- Since the angle subtended by AC at P is 90°, the angles ∠AOP and ∠COP are both 45° (because the diagonal bisects the angle at the center).
- The distance OA (from O to A) is A√2 (half the diagonal).
- The height of the pole is h, so we can use the Pythagorean theorem in triangle AOP:
AP2=AO2+OP2
AP2=(A√2)2+h2
AP2=A22+h2
- Now, consider the triangle ABP, where AB is a side of the square.
- Since OA = OB, the angle subtended by side AB at P will also be equal to the angle subtended by AC.
- Since triangle APB is isosceles (AP = PB), we can find the angle α subtended by side AB at P.
- The angles at P will be equal, and since the total angle around point P is 360°, we can deduce:
α+α+90°=180°
2α=90°
α=45°
- Therefore, the angle subtended by a side of the square at point P is 45°.
The angle subtended by a side of the square at P is 45°.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - OBJECTIVE RD SHARMACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise
45 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
- INCREASING AND DECREASING FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - INCREASING AND DECREASING FUNCTIONSEXERCISE - Chapter Test
20 Videos
Similar Questions
Each side of a square ABCD subtends an angle of 60∘ at the top of a tower of height h standing at the centre of a square. If a be the length of the side of the square, then
View SolutionA 10 meters high tower is standing at the centre of an equilateral triangle and each side of the triangle subtends an angle of 60∘ at the top of the tower. Then the length of each side of the triangle is.
View Solution
Knowledge Check
A vertical ple PO is standing at the centre O of a square ABCD. If AC subtends an ∠90∘ at the top P of the pole, then the anlge subtended by a side of the square at P is
A30∘B45∘C60∘DNone of theseA vertical pole AB is standing at the centre B of a square PQRS . If PR subtands an angle of 90∘ at the top , A of the pole , then the angle subtended by a side of the square at A is :
A30∘B45∘C60∘DNone of theseEach side of a square subtends an angle of 60∘ at the tip of a tower of height h metres standing at the centre of the square. If I is the length of each side of the square, then what is h2 equal to ?
A3a2=2h2B2a2=3h2C2h2=a2Dh2=2a2
A 10 meters high tower is standing at the center of an equilateral triangel and each side of the triangle subtends an angle of 60∘ at the top of the tower. Then the lengthof each side of the triangel is
View SolutionIn a circle with centre O an are ABC subtends an angle of 140∘ at the centre of the circle . The chord AB is produced to point P. Then ∠CBP is equal to :
View SolutionIn a circle with centre O. an arc ABC subtends an angle of 136∘ at the centre of the circle. The chord AB is produced to a point P. Then ∠CBP is equal to :
View SolutionA vertical pole stands at a point A on the boundary of a circular park of radius 2 km and subtends an angle 60∘ at another point B on the boundary. If the chord AB subtends the same angle 60∘ at the centre of the park, the height of the pole is

View SolutionIn the given figure, O is the centre of a circle and arc ABC subtends an angle of 130∘ at O. AB is extended to P, Then, ∠PBC is equal to
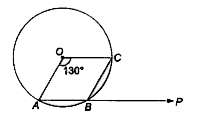
View Solution
