A vertical pole stands at a point O on a horizontal ground. A and B are points on the ground d metres apart. The pole subtends angles αandβ at A and B respectively. AB subtends an angle at O. the height of the pole is ______.
The correct Answer is:d[cot2α+cot2β−2cotαcotβcotγ]1/2
To find the height of the vertical pole at point O, we can use the concept of trigonometry. Let's denote the height of the pole as h.
1. Understanding the Geometry:
- Let the height of the pole be h.
- The distance from point A to the base of the pole (point O) is OA.
- The distance from point B to the base of the pole (point O) is OB.
- The distance between points A and B is given as d.
2. Using Trigonometric Ratios:
- From point A, the angle subtended by the pole is α. According to the tangent function:
tan(α)=hOA
Rearranging gives:
h=OA⋅tan(α)(1)
- From point B, the angle subtended by the pole is β. Similarly, we have:
tan(β)=hOB
Rearranging gives:
h=OB⋅tan(β)(2)
3. Relating OA and OB:
- Since A and B are d meters apart, we can express OA and OB in terms of d:
OA+OB=d
Let OA=x and OB=d−x.
4. Substituting in Equations:
- Substitute OA and OB into equations (1) and (2):
h=x⋅tan(α)(3)
h=(d−x)⋅tan(β)(4)
5. Setting Equations Equal:
- Since both expressions equal h, we can set them equal to each other:
x⋅tan(α)=(d−x)⋅tan(β)
6. Solving for x:
- Rearranging gives:
x⋅tan(α)+x⋅tan(β)=d⋅tan(β)
x(tan(α)+tan(β))=d⋅tan(β)
x=d⋅tan(β)tan(α)+tan(β)(5)
7. Finding Height h:
- Substitute x back into equation (3) to find h:
h=(d⋅tan(β)tan(α)+tan(β))⋅tan(α)
h=d⋅tan(α)⋅tan(β)tan(α)+tan(β)
Final Answer:
The height of the pole h is given by:
h=d⋅tan(α)⋅tan(β)tan(α)+tan(β)
- Let the height of the pole be h.
- The distance from point A to the base of the pole (point O) is OA.
- The distance from point B to the base of the pole (point O) is OB.
- The distance between points A and B is given as d.
- From point A, the angle subtended by the pole is α. According to the tangent function:
tan(α)=hOA
Rearranging gives:
h=OA⋅tan(α)(1)
tan(β)=hOB
Rearranging gives:
h=OB⋅tan(β)(2)
- Since A and B are d meters apart, we can express OA and OB in terms of d:
OA+OB=d
Let OA=x and OB=d−x.
- Substitute OA and OB into equations (1) and (2):
h=x⋅tan(α)(3)
h=(d−x)⋅tan(β)(4)
- Since both expressions equal h, we can set them equal to each other:
x⋅tan(α)=(d−x)⋅tan(β)
- Rearranging gives:
x⋅tan(α)+x⋅tan(β)=d⋅tan(β)
x(tan(α)+tan(β))=d⋅tan(β)
x=d⋅tan(β)tan(α)+tan(β)(5)
- Substitute x back into equation (3) to find h:
h=(d⋅tan(β)tan(α)+tan(β))⋅tan(α)
h=d⋅tan(α)⋅tan(β)tan(α)+tan(β)
The height of the pole h is given by:
h=d⋅tan(α)⋅tan(β)tan(α)+tan(β)
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - ML KHANNACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Problem Set (3) TRUE AND FALSE
11 Videos
- FUNCTIONSBOOK - ML KHANNACHAPTER - FUNCTIONSEXERCISE - SELF ASSESSMENT TEST
10 Videos
- INEQUALITIESBOOK - ML KHANNACHAPTER - INEQUALITIESEXERCISE - PROBLEM SET (1)(FILL IN THE BLANKS)
4 Videos
Similar Questions
Two circular path of radii a and b intersect at a point O and AB is a line through O meeting the circles at A and B respectively. Chords OA and OB subtend equal angles of 60∘ at their respective centres. A vertical pole at O subtends angles αandβ respectively at A and B then height of the pole is
View SolutionAB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is
View Solution
Knowledge Check
A vertical pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point β on the boundary. If the chord AB subtends an angle α at the centre of the park, the height of the pole is
A2a sinα2tanαB2a cosα2tanαC2a sinα2cotαD2a cosα2cotαA pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point B on the boundary. If the chord AB subtends an angle α at the centre of the path, the height of the pole is
A2acos(α/2)tanαB2asin(α/2)cotαC2asin(α/2)tanαD2acos(α/2)cotαAB is a vertical pole and C is its mid point. The end A is on the level ground and P is any point on the level ground other than A the portion CB substends an angle β at P. If AP:AB=2:1, then β=
Atan−149Btan−119Ctan−159Dtan−129
A vertical pole stands at a point A on the boundary of a circular park of radius 2 km and subtends an angle 60∘ at another point B on the boundary. If the chord AB subtends the same angle 60∘ at the centre of the park, the height of the pole is
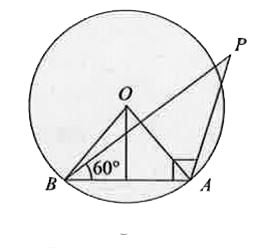
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View SolutionA tower of height b substends an angle at a point O on the leavel of the foot of the tower and at a distance a from the foot of the tower. If a pole mounted on the lower also subtends an equal angle at O, the height of the pole is
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View SolutionA lamp post standing at a point A on a circular path of radius r subtends an angle α at some point B on the path, and AB subtends an angle of 45∘ at any other point on the path, then height of the lampost is
View Solution
