A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in figure. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical partition has a diameter of 5 cm, while the base diameter of the cylindrical protion is 3 cm.
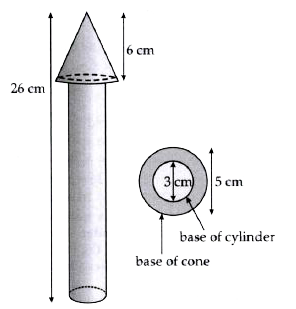
If the conical portion is to be painted orange, find the area to be painted orange. Find the area of the rockeeet peainted with each of these colours? (Take π = 3.14)
The correct Answer is:Area painted red = 58.143 cm2, Area painted white = 264 cm2
Step by step video & image solution for A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in figure. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical partition has a diameter of 5 cm, while the base diameter of the cylindrical protion is 3 cm. If the conical portion is to be painted orange, find the area to be painted orange. Find the area of the rockeeet peainted with each of these colours? (Take pi = 3.14) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VOLUME AND SURFACE AREAS OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREAS OF SOLIDSEXERCISE - Exercise 17B
35 Videos
- VOLUME AND SURFACE AREAS OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREAS OF SOLIDSEXERCISE - Exercise 17C
20 Videos
- VOLUME AND SURFACE AREAS OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREAS OF SOLIDSEXERCISE - Exercise 17A
28 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 12
15 Videos
Similar Questions
A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in figure. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical partition has a diameter of 5 cm, while the base diameter of the cylindrical protion is 3 cm.Find the slant height of conical portion.
View SolutionA wooden toy rocket is in the shape of a cone mounted on a cylinder as shown in Fig. 16.36. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π=3.14 )
View Solution
Knowledge Check
A solid is in the shape of a cone mounted on a hemisphere of same base readius. If the curved surface areas of the hemisphere part and the conical part are equal then find the ratio of the radius and the height of the conical part.
A1:3B1:√3C1:2Dnone of these
A wooden toy rocket is in the shape of a cone mounted on a cylinder. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours.
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside If the height of the cone is 24 cm the total height of the toy is 60 cm and the radius of the base of the cone= twice the radius of the base of the cylinder = 10 cm .Find the total surface area of the you.

View SolutionA toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, find the height of the toy
View SolutionA toy is in the form of a cone mounted on the hemisphere with the same radius. The diameter of the base of the conical portion is 12 cm and its height is 8 cm.
What is the volume of the toy?
View SolutionA tent is cylindrical in shape with a conical top above it. the radius of the base of tent is 7m. The height of the cylindrical part is 20m and the height of the conical part is 4m. Find the volume of air in the tent.
View SolutionThe height of a conical vessel is 3.5cm. If its capacity is 3.3 litres of milk. Find the diameter of its base.
View SolutionA wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 5cm and its height is 4cm. Find the cost of painting the toy at the rate of Rs. 5 per 1000cm2.
View Solution
