$A (6, 1), B (8, 2) and C (9, 4)$ are three vertices of parallelogram ABCD. If E is the mid-point of DC, then find the area of $Δ A D E$ .

Text Solution

Verified by Experts

Let the co-ordinates of point D be $(x_{4}, y_{4})$
Now, the mid-point of BD = mid-point of AC
$\Rightarrow (\frac{x_{4} + 8}{2}, \frac{y_{4} + 2}{2}) = (\frac{6 + 9}{2}, \frac{1 + 4}{2})$

$\Rightarrow \frac{x_{4} + 8}{2} = \frac{15}{2} \Rightarrow x_{4} = 7$
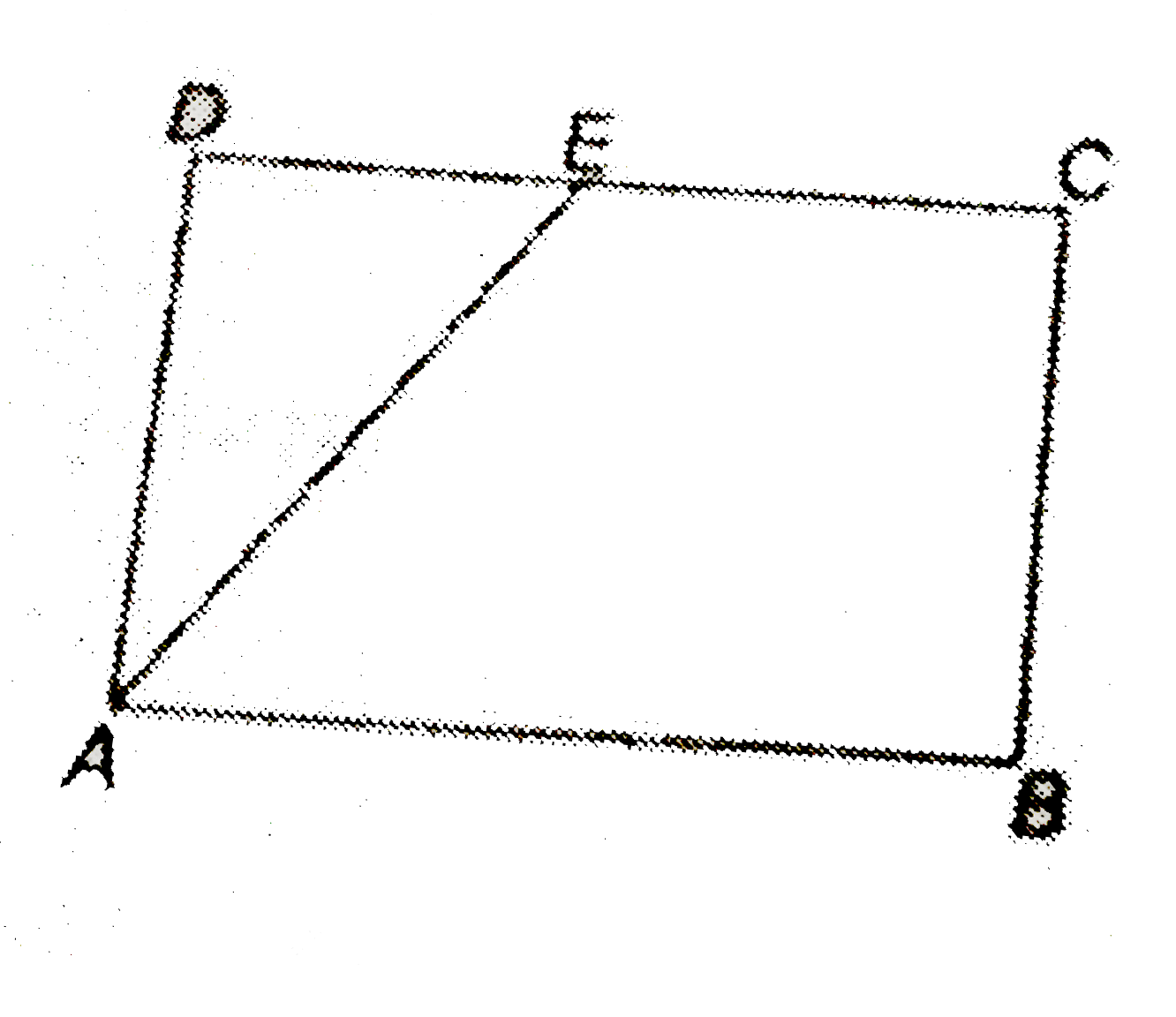
and $\frac{y_{4} + 2}{2} = \frac{5}{2} \Rightarrow y_{4} = 3$
$∴ D \equiv (7, 3)$
Mid-point E of CD $\equiv (\frac{7 + 9}{2}, \frac{3 + 4}{2}) \equiv (8, \frac{7}{2})$
Now, area of $Δ A D E = \frac{1}{2} [6 (3 - \frac{7}{2}) + 7 (\frac{7}{2} - 1) + 8 (1 - 3)] = \frac{1}{2} (- 3 + \frac{35}{2} - 16) = - \frac{3}{4}$
$∴$ Area of $Δ A D E = \frac{3}{4}$ square units (neglecting negative sign)

Updated on:21/07/2023