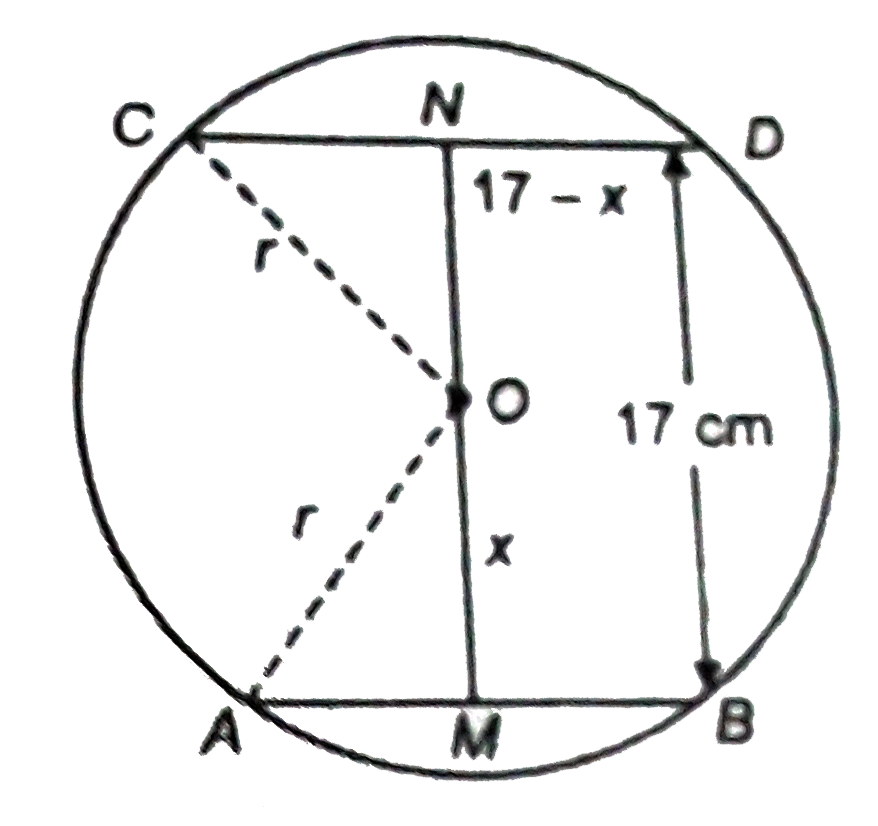
AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10 cm, CD=24 cm and the distance between AB and CD is 17 cm.Find the radius of the circle.

Video Solution

Text Solution

Verified by Experts

In the adjoining figure, O is the centre of the circle.
Here, $A B = 10 c m$
$C D = 24 c m$
OM and ON are perpendicular from centre $O$ to AB and CD respectively.
$∵ A B ∣ ∣ C D$
$∴$ MON is a transversal
Now, $A M = \frac{1}{2} A B = \frac{1}{2} \times 10 = 5 c m$
$C N = \frac{1}{2} C D = \frac{1}{2} \times 24 = 12 c m$
Let $O M = x$
$∴ O N = 17 - x$
In $Δ O M A$ ,
$O A^{2} = O M^{2} + A M^{2}$ (where $O A = r$ is the radius of circle)
$\Rightarrow r^{2} = x^{2} + 5^{2}$ ........(1)
$∴$ In $Δ O C N$ ,
$O C^{2} = O N^{2} + C N^{2}$
$\Rightarrow e^{2} = {(17 - x)}^{2} + 12^{2}$ .........(2)
From eqs. (1) and (2).
$x^{2} + 5^{2} = {(17 - x)}^{2} + 12$
$\Rightarrow x^{2} + 25 = 289 + x^{2} - 34 x + 144$
$\Rightarrow 34 x = 289 + 144 - 25$
$= 408$
$\Rightarrow x = \frac{408}{34} = 12$
Put $x = 12$ in eq. (1)
$r^{2} = x^{2} + 5^{2}$
$= 12^{2} + 5^{2}$
$= 144 + 25$
$= 169$
$\Rightarrow r = \sqrt{169} = 13 c m$
$∴$ Radius of circle =13cm.

Updated on:21/07/2023