AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB =10cm , CD =24 cm and the distance between AB and CD is 17cm. Find the radius of the circle.
13 cm
14 cm
15 cm
16 cm
The correct Answer is:A
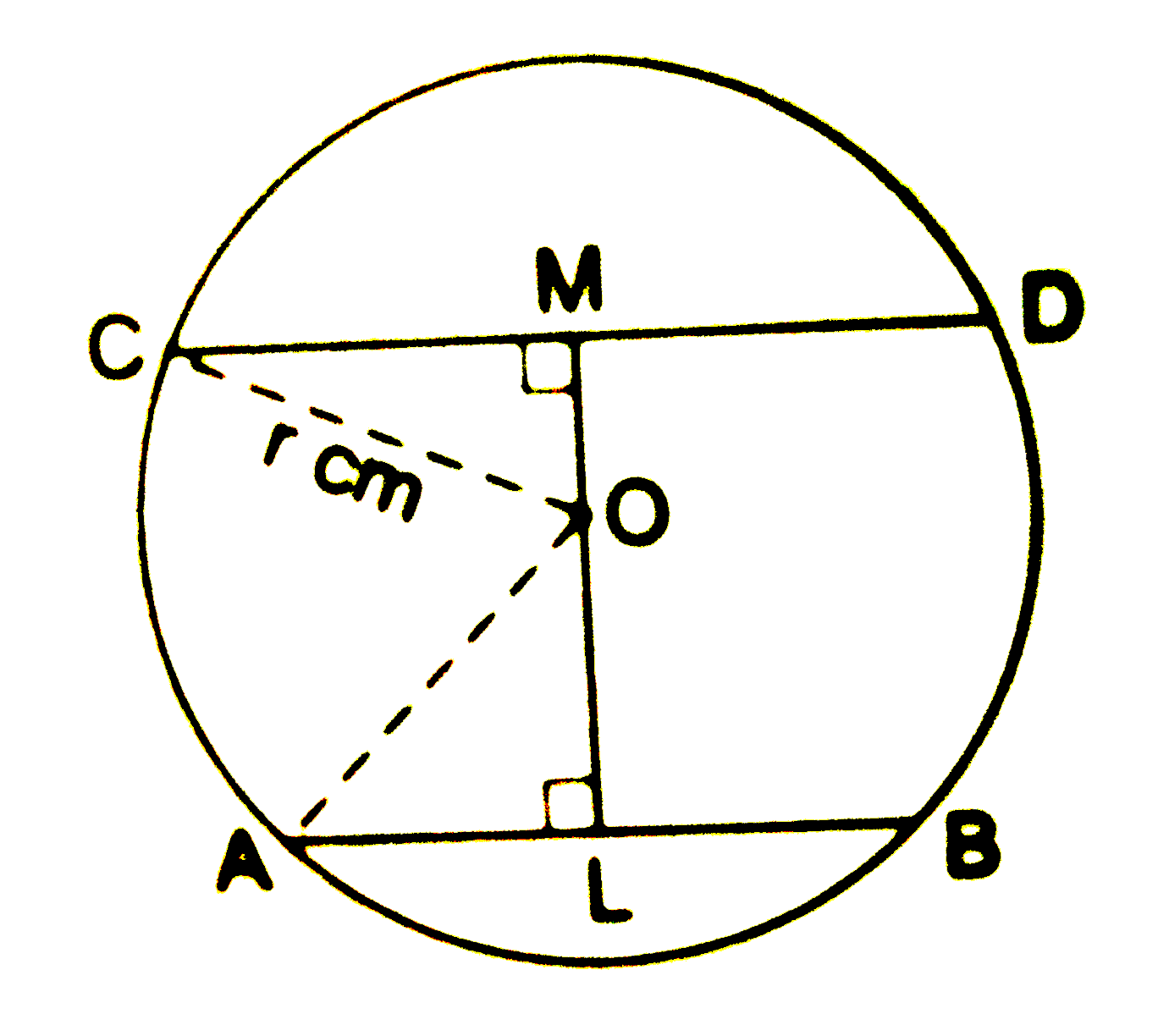
Let AB and CD be two chords of a circle C(O,r) such that AB∣∣CD. Also , AB =10cm and CD=24cm.
Draw OL ⊥ AB and OM ⊥CD
Join OA and OC .
Then , OA = OC =r cm
Since OL ⊥ AB and OM ⊥ CD and AB∣∣CD , the points L,O,M are collinear
∴LM=17cm
Let Ol = X cm . Then, OM =(17−X)cm.
Since the perpendicular from the centre of a circle to a chord bisects the chord, we have
AL=12AB−(12×10)cm=5cm, and CM=12CD=(12×24)cm=12cm.
From the right ΔOLA, we have
OA2=OL2+AL2⇒r2=x2+(5)2. ....(i)
From the right ΔOMC, we have
OC2=OM2+CM2⇒r2=(17−x)2=(12)2. ....(ii)
From (i) and (ii) , we get
x2+(5)2=(17−x)2+(12)2
⇔x2+25=x2−34x+433
⇔34x=408⇔x=12
Putting x=12 in (i) , we get r2=169⇒r=13
Hence, the radius of the circle is 13 cm.
Similar Questions
AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10cm, CD=24cm and the distance between AB and CD is 17cm. Find the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10 cm, CD=24 cm and the distance between AB and CD is 17 cm.Find the radius of the circle.
View Solution
Knowledge Check
AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB =10cm , CD =24 cm and the distance between AB and CD is 17cm. Find the radius of the circle.
A13 cmB14 cmC15 cmD16 cmAB and CD are two chords of a circle such that AB = 10 cm, CD - 24 cm and AB||CD. If the distance between AB and CD is 17 cm. Then, the radius of the circle is equal to
A13B169C26Dnone of theseAB and CD are two chords of a circle such that AB = 10 cm, CD - 24 cm and AB||CD. If the distance between AB and CD is 17 cm. Then, the radius of the circle is equal to
A13B169C26DNone of these
In a circle with centre O. AB and CD are parallel chords lying on opposite sides of a diameter parallel to them. If AB = 30 cm, CD - 48 cm and the distance between AB and CD is 27 cm, find the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD.
View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD
View SolutionAB and CD are two parallel chords of a circle such that AB=10cm and CD=24cm. If the chords are on the opposite sides of the centre and the distance between them is 17cm, find the radius of the circle.
View SolutionAB and CD are two chords of a circle such that AB= 10 cm, CD = 24 cm and AB|| CD. The distance between AB and CD is 17 cm. Then, the radius of the circle is equal to
View Solution
