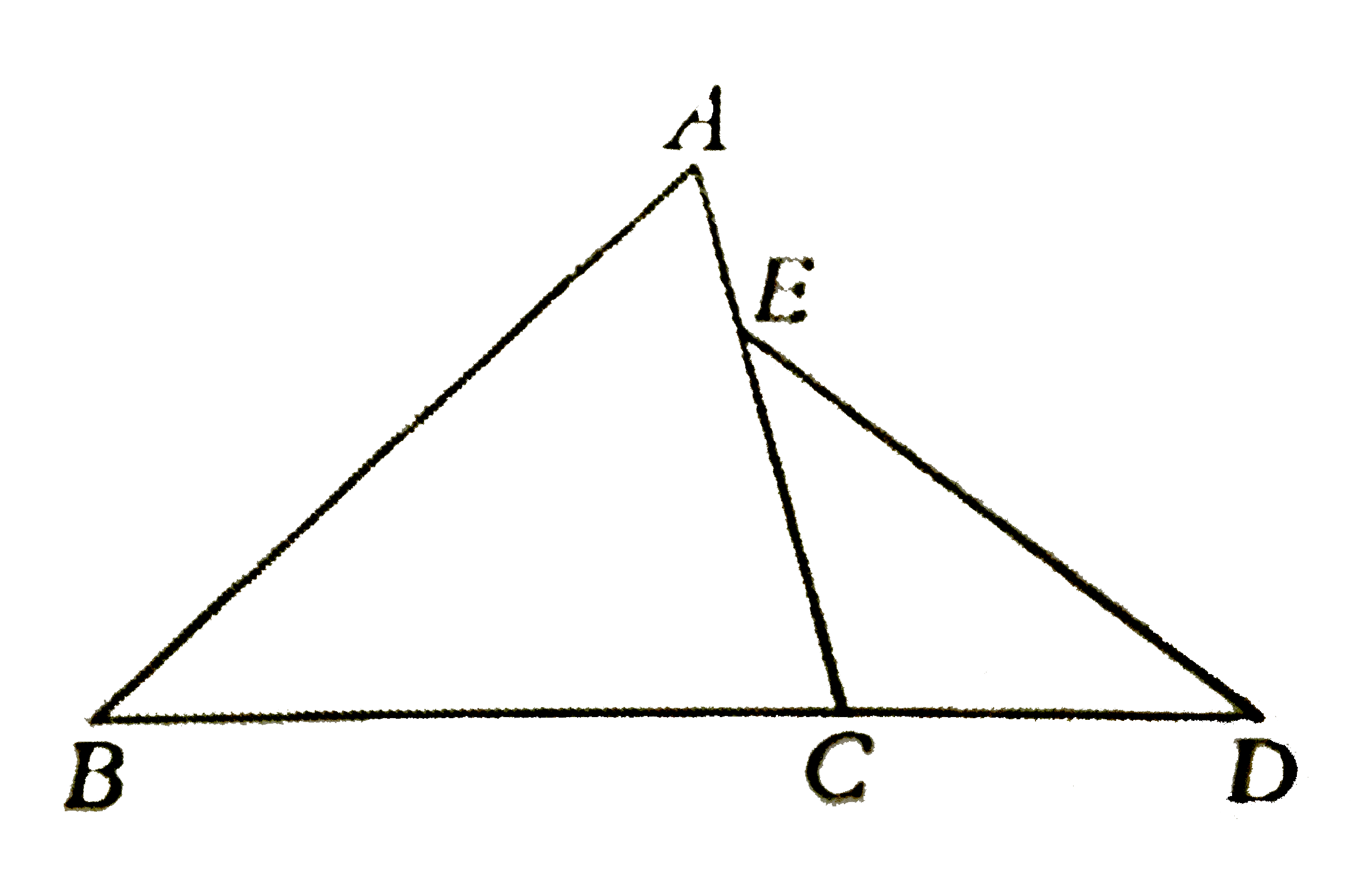
AB⊥BC,BD⊥ACandCE bisects ∠C.∠A=30∘. Then what is ∠CED?

30°
60°
45°
65°
The correct Answer is:B
Step by step video, text & image solution for AB bot BC , BD bot AC and CE bisects angle C. angle A = 30^(@). Then what is angle CED? by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - Self Assessment Sheet - 18
10 Videos
- TRIANGLESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - Self Assessment Sheet - 18
10 Videos
- TIME AND WORK BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TIME AND WORK EXERCISE - Self Assessment Sheet - 13
15 Videos
- VOLUME AND SURFACE AREA OF A CUBE AND A CUBOIDBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - VOLUME AND SURFACE AREA OF A CUBE AND A CUBOIDEXERCISE - UNIT TEST - 5
20 Videos
Similar Questions
Knowledge Check
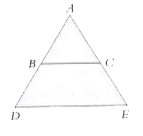
In the figure above BC∣∣DEand∠ABC=∠CED.∠A=∠ACB=30∘. Find ∠AA40∘B50∘C45∘D55∘In ΔABCBC⊥AC at D.E is a point on BC such that ∠BEA=x∘ If ∠EAC=36∘and∠EBD=40∘, then the value of x is:
A68∘B86∘C72∘D78∘In △ABC,BD⊥AC. E is a point on BC such that ∠BEA = x . If ∠EAC = 38 and ∠EBD=40∘, then the value of x is:
A88∘B68∘C78∘D72∘
In △ABC,BD⊥AC, at D,E is a point on BC such that ∠BEA=x∘. If ∠EAC=62∘ and ∠EBD=60∘, then the value of x is :
त्रिभुज ABC में, BD⊥AC पर D, E, BC पर एक बिंदु है जेसे कि ∠BEA=x∘ यदि ∠EAC=62∘ और ∠EBD=60∘ है, तो x का मान है :
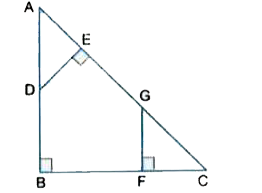
View SolutionIn the given fig; AB⊥BC,FG⊥BC, and DE⊥AC. Prove that △ADE~△GCF.
View SolutionIn △ABC,BE⊥AC,CD⊥AB and BE and CD intersect each other at O. The bisectors of ∠OBC and ∠OCB meet at P. If ∠BPC=148∘, then what is the measure of ∠A ?
त्रिभुज ABC में, BE⊥AC,CD⊥AB तथा BE और CD एक दूसरे को O पर काटती हैं | ∠OBC तथा ∠OCB के समद्विभाजक P पर मिलते हैं | यदि ∠BPC=148∘ है, तो कोण A का मान क्या है?
View Solution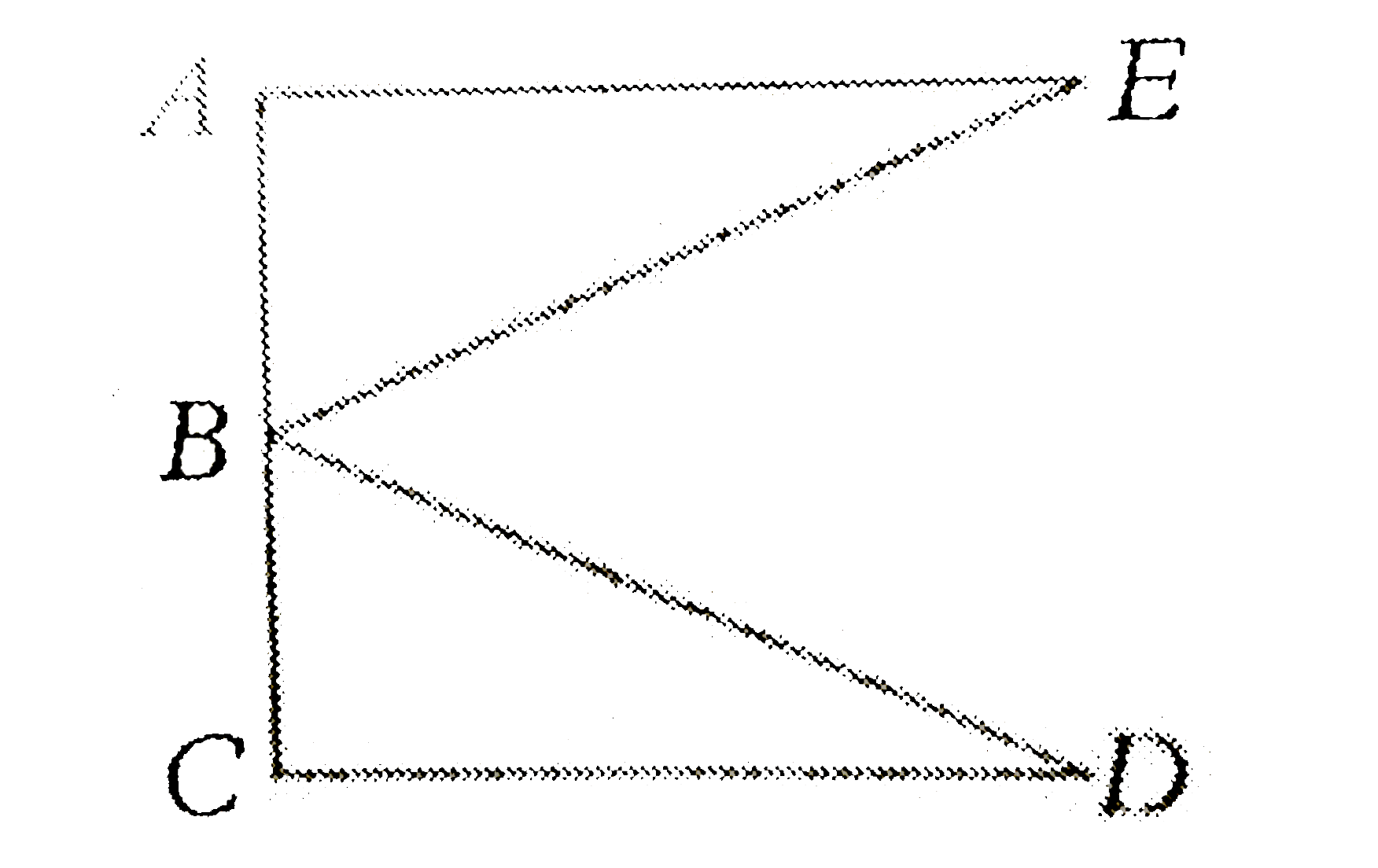
In the given figure, ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯CD, AB=BC, and AE=CD. If ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CDand∠AEB=35∘, then find ∠DBE.
View SolutionThat AD|| BE,AB ⊥ AD ∠DCE=85∘,∠BDC=30∘ what is the of x ?
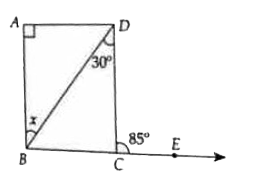
View Solution