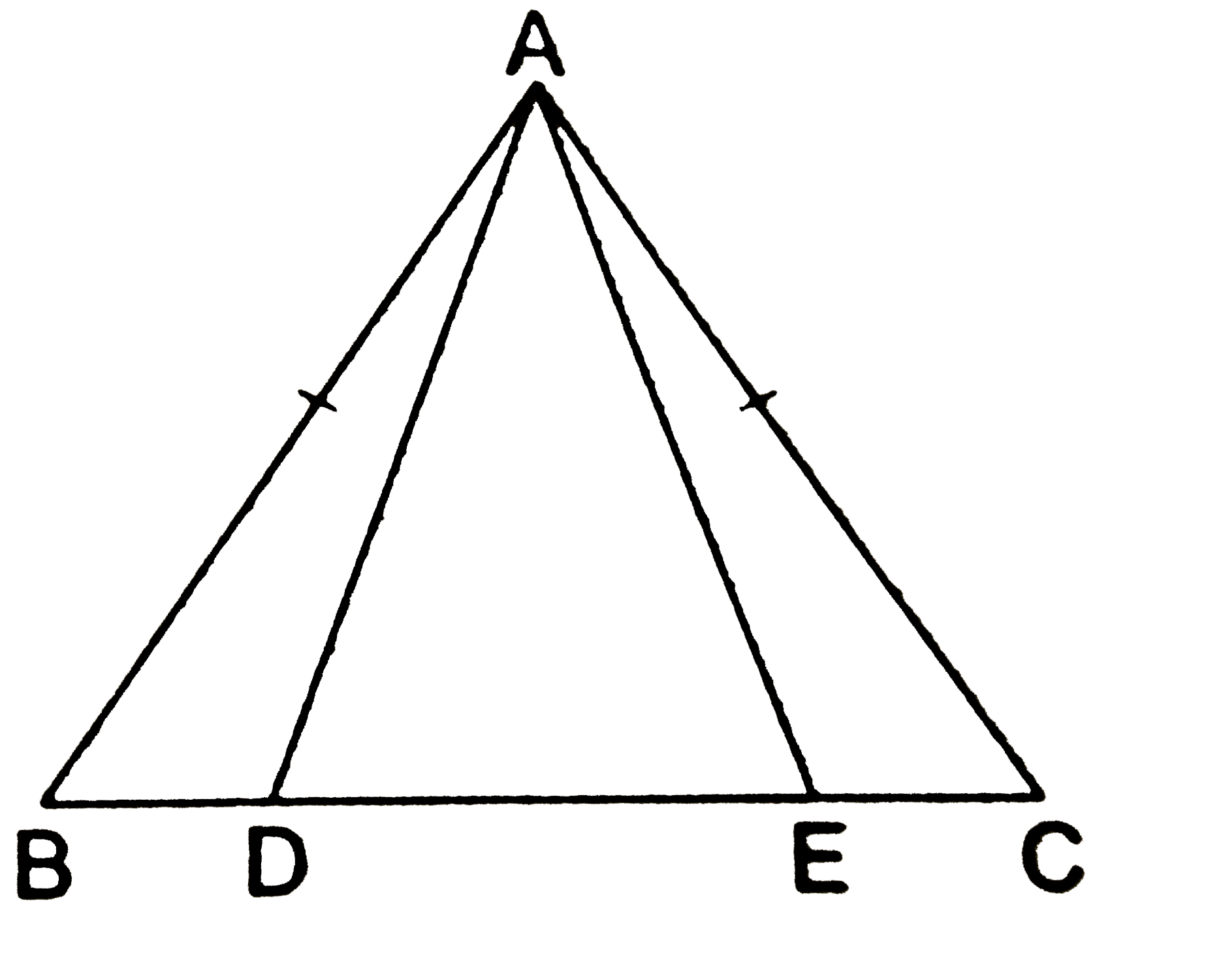
ABC is a triangle. D is a point on AB such that AD=14ABandE is a point an AC such that AE=14AC. Then DE=_______
BC
2 BC
14 BC
12 BC
The correct Answer is:C
To solve the problem, we need to find the length of segment DE in triangle ABC given the points D and E on sides AB and AC respectively.
1. Identify the Points:
- Let A, B, and C be the vertices of triangle ABC.
- Point D is on side AB such that AD=14AB.
- Point E is on side AC such that AE=14AC.
2. Express Lengths:
- Let AB=c and AC=b.
- Then, AD=14c and AE=14b.
3. Use Similar Triangles:
- Triangles ADE and ABC are similar because they share angle A and both have corresponding angles equal (angle DAE and angle BAC).
- Therefore, we can set up a ratio of corresponding sides:
ADAB=AEAC=DEBC
4. Substituting Known Values:
- From the similarity, we know:
ADAB=1/4⋅cc=14
AEAC=1/4⋅bb=14
- Thus, we can write:
DEBC=14
5. Finding DE:
- Rearranging gives us:
DE=14BC
Final Answer:
Thus, the length of segment DE is 14BC.
- Let A, B, and C be the vertices of triangle ABC.
- Point D is on side AB such that AD=14AB.
- Point E is on side AC such that AE=14AC.
- Let AB=c and AC=b.
- Then, AD=14c and AE=14b.
- Triangles ADE and ABC are similar because they share angle A and both have corresponding angles equal (angle DAE and angle BAC).
- Therefore, we can set up a ratio of corresponding sides:
ADAB=AEAC=DEBC
- From the similarity, we know:
ADAB=1/4⋅cc=14
AEAC=1/4⋅bb=14
- Thus, we can write:
DEBC=14
- Rearranging gives us:
DE=14BC
Thus, the length of segment DE is 14BC.
Topper's Solved these Questions
- IMO QUESTION PAPER 2018 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET AEXERCISE - EVERYDAY MATHEMATICS
10 Videos
- IMO QUESTION PAPER 2017 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET BEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2018 SET B BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET B EXERCISE - Achievers Section
5 Videos
Similar Questions
Knowledge Check
For a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
Aa) 5 cmBb) 4 cmCc) 3 cmDd) 6 cmFor a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
A5 cmB4 cmC3 cmD6 cm
ABC is a triangle right angled at B. D is a point on AC such that ∠ABD=45∘ If AC=6 and AD=2 then AB=
View SolutionIn a ΔABC,AB=AC,D is a point BC such that ∠BAD=50∘ and a point E on side AC such that AE =AD find ∠CDE
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
View SolutionIn an isosceles ΔABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
View SolutionIn figure, ABC is a triangle with ∠B=90∘, BC = 3cm and AB = 4cm. D is a point on AC such that AD = 1cm and E is the mid- point of AB. Join D and E and extend DE to meet CB extended at F. Then BF is equal to
View Solution
