ABC is a triangle in a plane with vertices $A (2, 3, 5), B (- 1, 3, 2)$ and $C (λ, 5, μ)$ . If the median through A is equally inclined to the coordinate axes, then the value of $λ^{3} + μ^{3} + 5$ is

A

676

B

1130

C

1348

D

1077

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let $D$ be the mid-point of side BC of $Δ A B C$ . The coordinate of D are $(\frac{λ - 1}{2}, 4, \frac{μ + 2}{2})$ .
So direction of $- - \to A D$ are proportional to $\frac{λ - 5}{2}, 1, \frac{μ - 8}{2}$ and its direction cosines are
$\frac{λ - 5}{2 k}, \frac{1}{k}, \frac{μ - 8}{2 k}$ where $k = \sqrt{{(\frac{λ - 5}{2})}^{2} + 1 + {(\frac{m 8 - u}{2})}^{2}}$

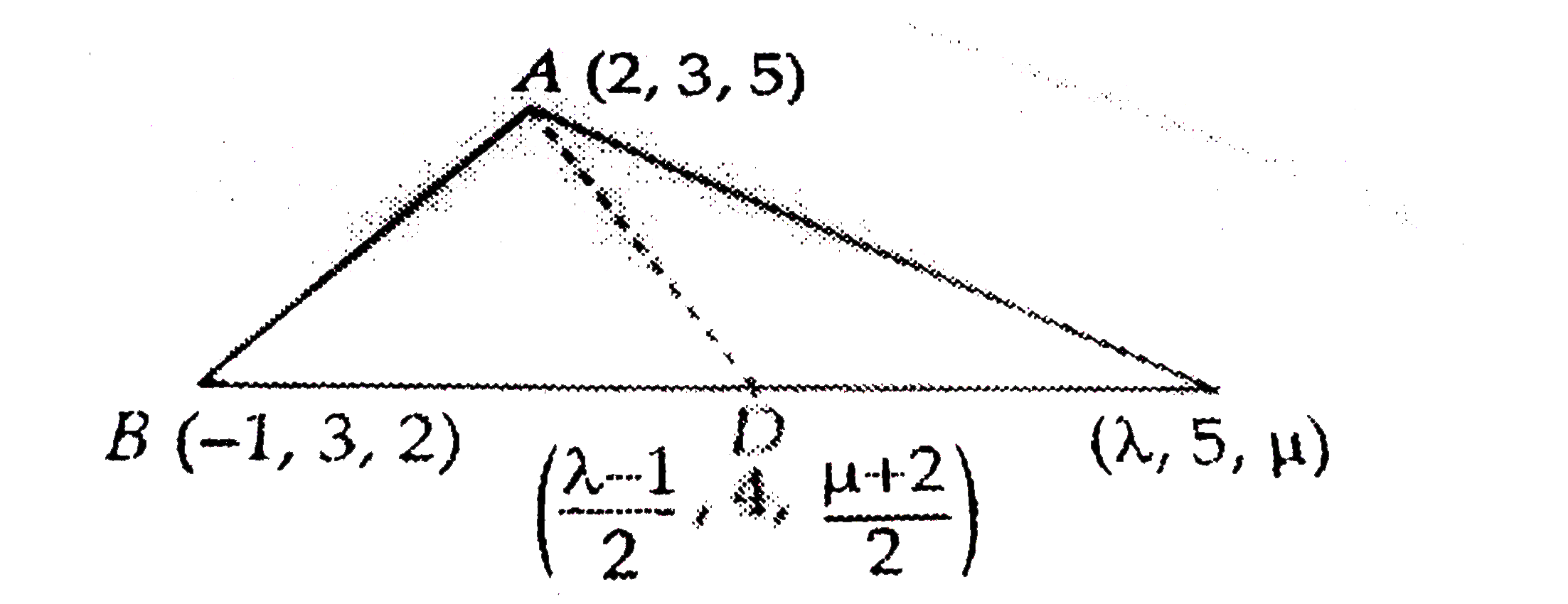
It is given that AD is equally inclined to the coordinates axes.
$∴ \frac{λ - 5}{2 k} = \frac{1}{k} = \frac{μ - 8}{2 k} = \pm \frac{1}{\sqrt{3}}$
$\Rightarrow λ - 5 = 2 μ - 8 = 2 \Rightarrow λ = 7, μ = 10$
$∴ λ^{3} + 5 = 7^{3} + 10^{3} + 5 = 1348$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$A (2, 3, 7), B (- 1, 3, 2), C (p, 5, r)$ are vertices of $Δ A B C$ . If the median through A is equally inclined to the co-ordinate axes, then the values of p and r are
A $7, 14$
B $14, 7$
C $7, 7$
D $14, 14$
Question 2 - Select One
Let ABC be a triangle with vertices at points A (2,3,5), B (-1,3,) and $C (λ, 5, μ)$ in three dimensional space. If the median through A is equally inclined with the axes, then $(λ, μ)$ is equal to :
A $(10, 7)$
B $(7, 5)$
C $(7, 10)$
D $(5, 7)$
Question 3 - Select One
Suppose A(2,3,7), B(-1,3,2) and C(p,s,r) are the vertices of $Δ A B C$ . If the median through A is equally inclined to the coordinate axes then the coordinates of the vertex C is
A(7,5,12)
B(7,5,16)
C(7,5,14)
DNone of these

OBJECTIVE RD SHARMA-THREE DIMENSIONAL COORDINATE SYSTEM -Exercise

Home
Ask Doubt
Profile