ABC is an isosceles triangle inscribed in a circle of radius r. If AB=AC and h is the altitude form A to BC. If P is perimeter and A is the area of the triangle then find the value of limh→0AP3.
In ΔABC,AB=AC,AD⊥BC(D is midpoint of BC)
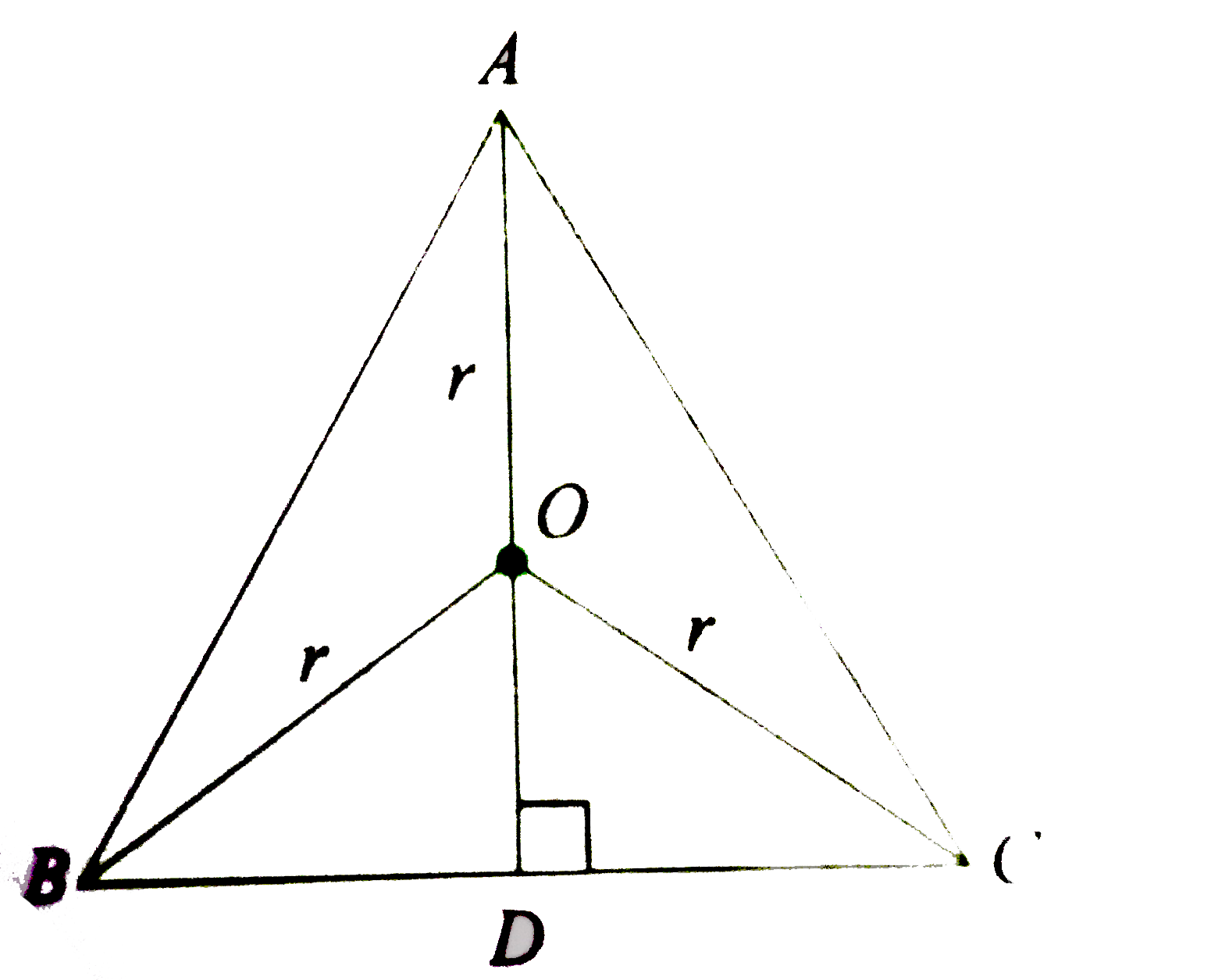
Let r= radius of circumcircle
∴ OA=OB=OC=r
Now BD=√BO2−OD2=√r2−(h−r)2=√2rh−h2
∴ BC=2√2rh−h2
AlsoAB2=BD2+AD2=2hr−h2+h2=2hr.
∴ AB=AC=√2hr
∴ Perimeter,P=2√2rh−h2+2√2hr
∴ Area of ΔABC=12×BC×AD=h√2rh−h2
So, limh→0AP3=h√2rh−h28(√2rh−h2+√2hr)3
=limh→0h3/2√2r−h8h3/2(√2r−h+√2r)3
=limh→0√2r−h8[√2r−h+√2r]3
=√2r8(√2r+√2r)3=1128r
Topper's Solved these Questions
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.1
10 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.2
7 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
ABC is an isosceles triangle inscribed in a circle of radius r , if AB = AC and h is the altitude from A to BC . If the △ABC has perimeter P and △ then limh→0512rΔp3 equals
View SolutionABC is an isosceles triangle inscribed in a circle of radius r , if AB = AC and h is the altitude from A to BC . If the △ABC has perimeter P and △ is area then limh→0512rΔp3 equals
View Solution
Knowledge Check
ABC is an isosceles triangle inscribed in a circle. If AB=AC12√5 and BC = 24 cm then radius of circle is:
A10 cm.B15 cm.C12 cm.D14 cm.
ABC is an isosceles triangle described in a circle of radius r.If AB=AC and h is the altitude from A toBC, then limh→0Δp3 equals to [where A is the arca and P is the perimeter of the triangle ABC]
View SolutionABC is an isosceles triangle inscribed in a circle. If AB=AC12√5 and BC = 24 cm then radius of circle is:
View SolutionABC is an isosceles triangle inscribed in a circle of radius r. If AB=AC and h is the altitude from A to BC, then triangle ABC has perimeter P=2(√2hr−h2+√2hr) and area A= ____________ and = __________ and also (lim)h→0AP3=____
View SolutionABC is an isosceles triangle inscribed in a circle of radius r. If AB=AC and h is the altitude from A to BC, then triangle ABC has perimeter P=2(√2hr−h2+√2hr) and area A= ____________ and = __________ and also (lim)x→0AP3=____
View SolutionABC is an isosceles triangle inscribed in a circle of radius r. If AB=AC and h is the altitude from A to BC, then triangle ABC has perimeter P=2(√2hr−h2+√2hr) and area A= ____________ and = __________ and also (lim)x→0AP3=____
View SolutionIf an isosceles triangle ABC in which AB=AC=6cm is inscribed in a circle of radius 9cm, find the area of the triangle.
View SolutionABC is an isosceles right angle Δ . If Perimeter is P find Area
View Solution
