ABCD is a cyclic quadrilateral in a circle with centre O.
If ∠ADC=130∘ , find angle BAC ?
To solve the problem step by step, we will use properties of cyclic quadrilaterals and angles in a circle.
Step 1: Identify the given information
We are given that ∠ADC=130∘ in the cyclic quadrilateral ABCD.
Hint: Remember that in cyclic quadrilaterals, opposite angles sum up to 180∘.
Step 2: Use the property of cyclic quadrilaterals
Since ABCD is a cyclic quadrilateral, we can use the property that the sum of the opposite angles is 180∘. Thus, we have:
∠ABC+∠ADC=180∘
Substituting the known value:
∠ABC+130∘=180∘
Hint: This step helps us find the angle opposite to the given angle.
Step 3: Solve for ∠ABC
Now, we can isolate ∠ABC:
∠ABC=180∘−130∘=50∘
Hint: This calculation gives us the angle adjacent to the angle we need to find.
Step 4: Use the property of angles in a semicircle
Next, we know that ∠ACB is an angle in a semicircle, which means:
∠ACB=90∘
Hint: Remember that any angle subtended by a diameter of a circle is a right angle.
Step 5: Apply the triangle sum property
In triangle ABC, the sum of angles is 180∘:
∠BAC+∠ABC+∠ACB=180∘
Substituting the known values:
∠BAC+50∘+90∘=180∘
Hint: This step is crucial as it leads us to the angle we need to find.
Step 6: Solve for ∠BAC
Now, we can isolate ∠BAC:
∠BAC+140∘=180∘
∠BAC=180∘−140∘=40∘
Final Answer
Thus, the measure of ∠BAC is 40∘.
---
We are given that ∠ADC=130∘ in the cyclic quadrilateral ABCD.
Since ABCD is a cyclic quadrilateral, we can use the property that the sum of the opposite angles is 180∘. Thus, we have:
∠ABC+∠ADC=180∘
Substituting the known value:
∠ABC+130∘=180∘
Now, we can isolate ∠ABC:
∠ABC=180∘−130∘=50∘
Next, we know that ∠ACB is an angle in a semicircle, which means:
∠ACB=90∘
In triangle ABC, the sum of angles is 180∘:
∠BAC+∠ABC+∠ACB=180∘
Substituting the known values:
∠BAC+50∘+90∘=180∘
Now, we can isolate ∠BAC:
∠BAC+140∘=180∘
∠BAC=180∘−140∘=40∘
Thus, the measure of ∠BAC is 40∘.
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
ABCD is a cyclic quadrilateral in which BC is paralleld to AD, angle ADC=110∘ and angle BAC=50∘. Find angle DAC and angle DCA.
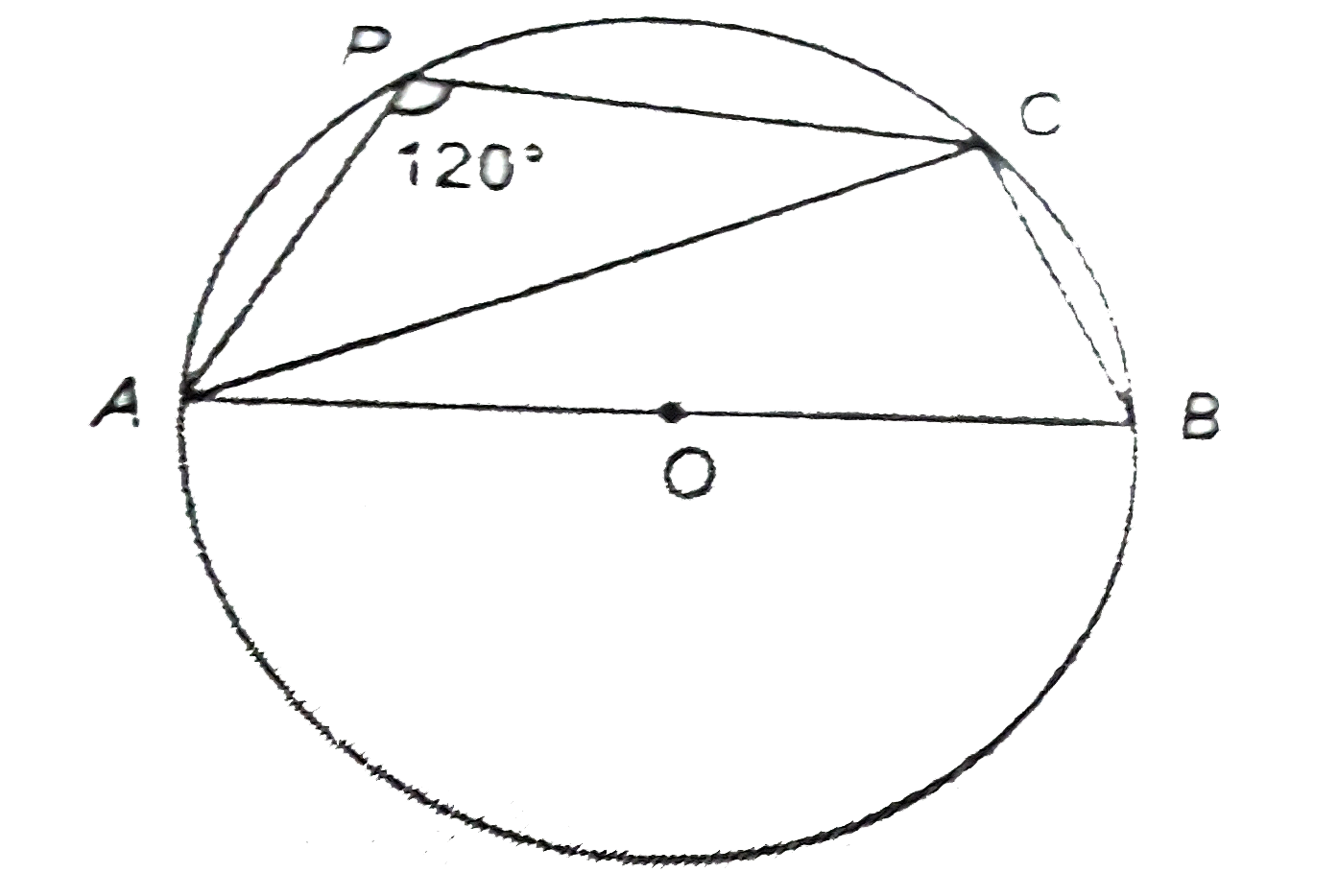
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
View SolutionIn cyclic quadrilateral ABCD , AD = BC, ∠BAC=30∘and∠CBD=70∘ , find : angle ADC .
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠BCD
View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠BCA
View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠ABC
View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View SolutionIn Figure, ABCD is a cyclic quadrilateral; O is the centre of the circle. If ∠BOD=1600, find the measure of ∠BPD
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
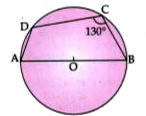
∠BCD=130∘. Find
(i) ∠DAB
View Solution
