ABCD is a reactangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B
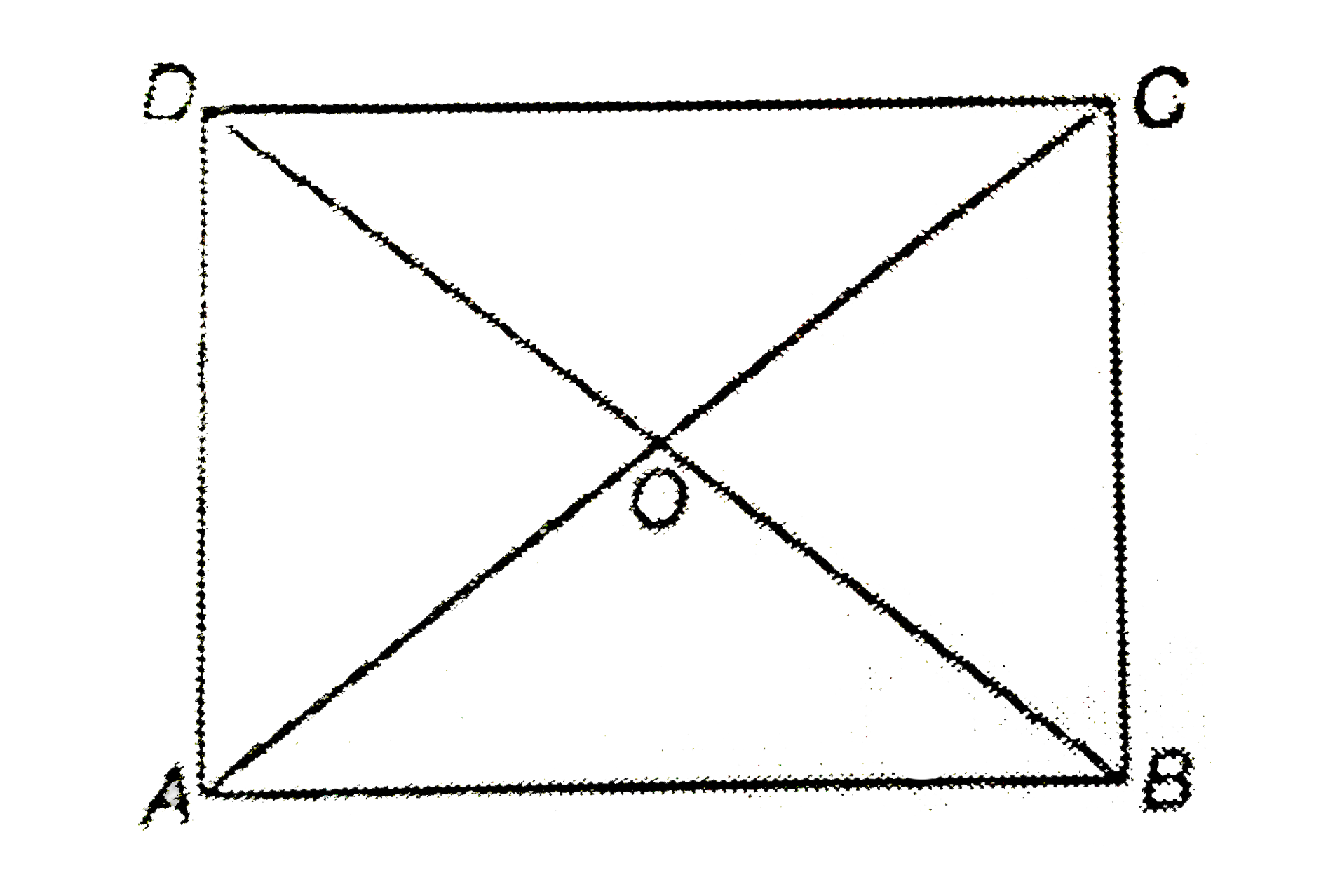
Step by step video & image solution for ABCD is a reactangle in which diagonal AC bisects angleA as well as angleC. Show that (i) ABCD is a square (ii) diagonal BD bisects angleB by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - NCERT SECTION (Exercise 8.2 )
11 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-1 )
35 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - SOLVED EXAMPLES
12 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Knowledge Check
If in a rectangle ABCD, diagonal AC bisect ∠A as well as ∠C then ABCD is a
AParallelogramBsquareCRhombusDTrapeziumThree statements are given below:
I. In a rectangle ABCD, the diagonal AC bisects ∠A as well as ∠C.
II. In a square ABCD, the diagonal AC bisects ∠A as well as ∠C.
III. In a rhombus ABCD, the diagonal AC bisects ∠A as well as ∠C.
Which is true?AI onlyBII and IIICI and IIIDI and IIABCD is a quadrlateral in which BD and AC are diagonals then
AAB+BC+CD+AD<AC+BDBAB+BC+CD+DA>AC+BDCAB+BC+CD+DA=AC+BDDAB+BC+CD+DA>2(AC+BD)
ABCD is a rectangle in which diagonal BD bisects ∠B. Show that ABCD is a square.
View SolutionABCD is a parallelogram and AE and CF bisect ∠Aand∠C respectively. Prove that AE||FC.

View SolutionIf ABCD is a quadrilateral whose diagonals AC and BD intersect at O, then

View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠B as well as ∠D.
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
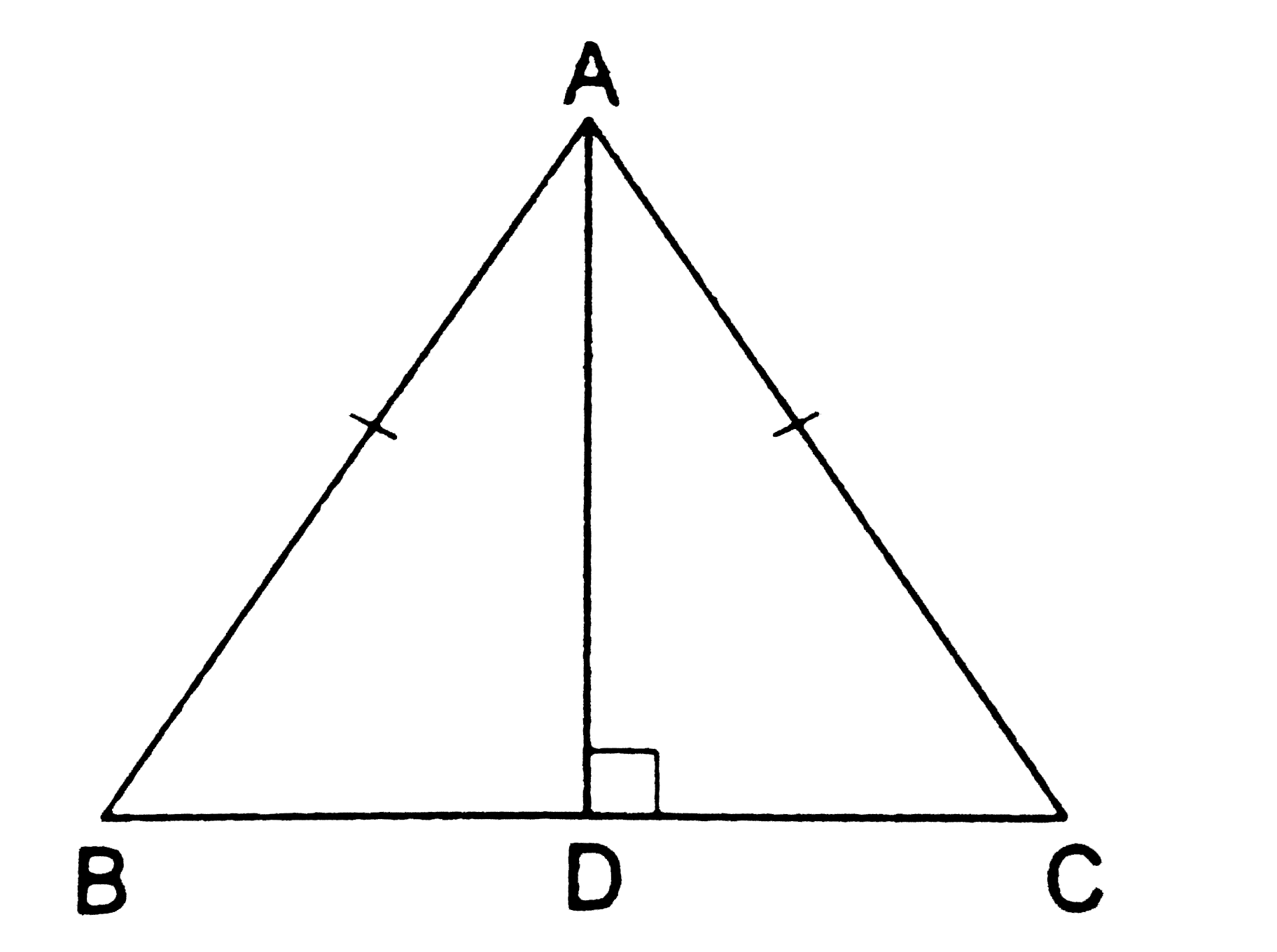
View Solution
