ABCD is a rectangle whose three vertices are B(4, 0), C(4, 3) and D(0, 3). The length of one of its diagonals is
A
5
B
4
C
3
D
25
Video Solution
Text Solution
The correct Answer is:A
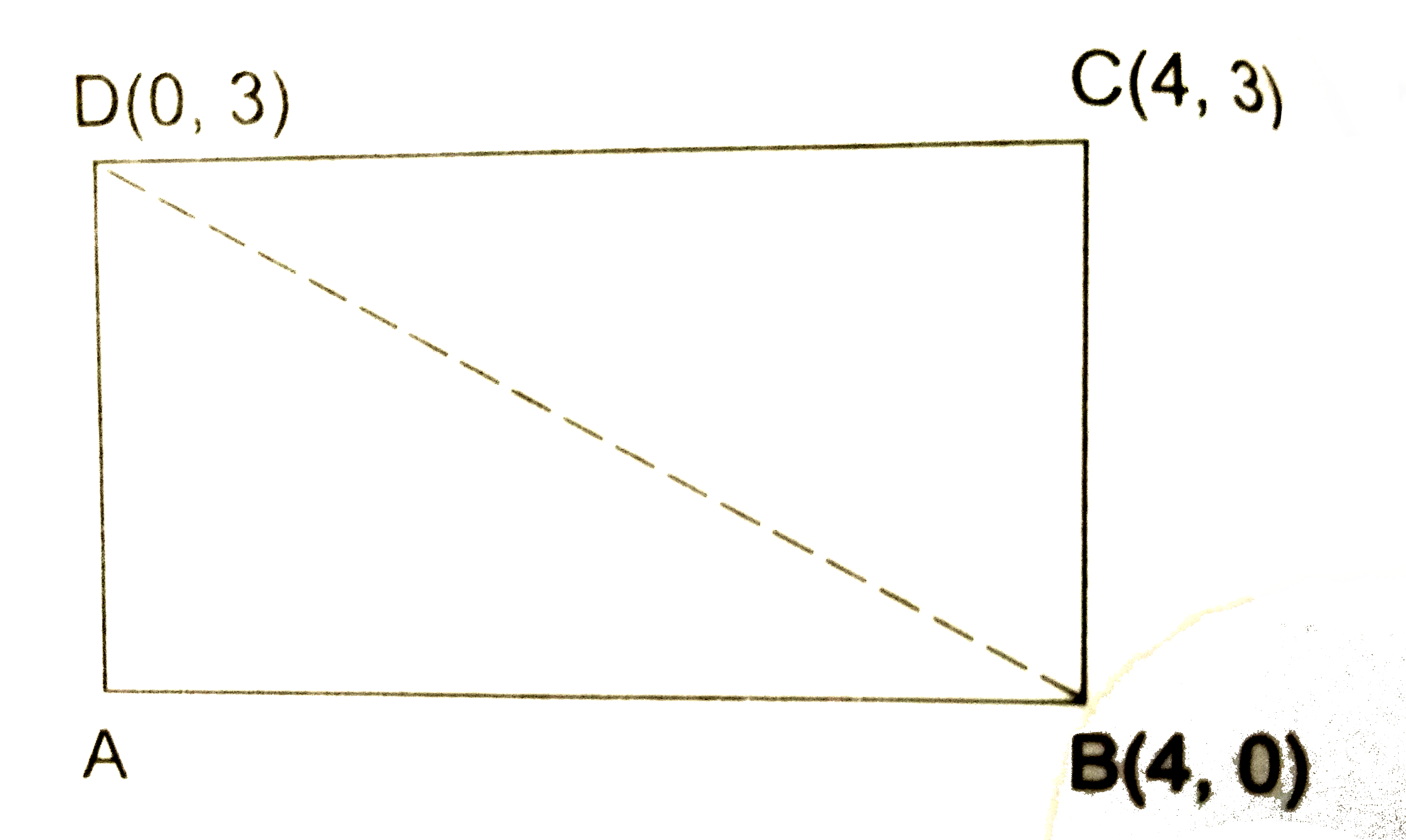
Diagonal BD=√(4−0)2+(0−3)2=√16+9
=√25=5 units.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 6D17videos
COORDINATE GEOMETRY
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)25videos
HEIGHTS AND DISTANCES
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a rectangle whose three vertices are A (0,4) B (0,0) and C (3,0) . The length of its diagonal is
A5B3C6D4 - Question 2 - Select One
If AOBC is a rectangle whose three vertices are A(0,3),O(0,0) and B(5,0), then find the length of its diagonal.
A5B3C√34D4 - Question 3 - Select One
Orthocentre of triangle whose vertices are (0,0),(3,4),(4,0) is
A(3,73)B(3,54)C(5,−2)D(3,34)
The vertices of a reactangle ABCD are A(−1,0)B(2,0),C(a,b)andD(−1,4). Then the length of the diagonal AC is
View SolutionOrthocentre of triangle whose vertices are (0,0),(3,4),(4,0) is
View SolutionDraw a quadrilateral with vertices A (4, 3), B(-4, 3), C(-4, -3) and D(4, -3). Draw its diagonals and write the coordinates of the point where the diagonals cut each other?
View SolutionThe area of the triangle whose vertices are A(1,2−1) B (3,1,4) and C (0,2,3)
View SolutionThe incentre of triangle whose vertices are A(0,3,0),B(0,0,4),C(0,3,4) is
View Solution

